Question

What is the direction of the velocity of the ball at point $P$ ?

A. $\to$
B. $\leftarrow$
C. $\downarrow$
D. $\uparrow$

Answer 1

The direction of linear velocity in a circular motion always changes. Learn about circular motion, angular velocity and the relation between angular velocity and linear velocity to solve the problem.

Formula used:
The angular velocity of any body is related to linear velocity as,
$v = w \times r$
where, $v$ is the linear velocity vector $r$ is the radius vector or the position vector and $w$ is the angular velocity vector.

Complete step by step answer:
We have given her a body which is rotating on a circular path with some angular velocity. Now, from the figure we can see that the direction of rotation is in clockwise direction. So, the angular velocity vector of the body must be inside the plane of paper, using the right hand screw rule. Now, the radius vector is along the radial direction away from the centre of the circular path. So, if we denote the angular velocity vector along the negative Z-axis and the radius vector in the X-Y plane along negative X axis, we can write,
$v = w\hat k \times r( - \hat i)$

So, performing the cross product we can have, $v = wr( - \hat j)$. So, that means the velocity vector will be along the negative Y-axis. So, if we redraw the diagram denoting the radius vector along X-axis we can see that the velocity vector is along the tangential direction.

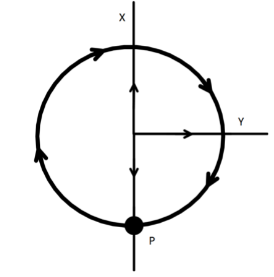
Hence, the velocity of the ball at $P$ is along $\leftarrow$ direction.

So, option B is the correct answer.

Note: If the ball is moving with constant angular velocity the magnitude of the linear acceleration will be a constant but as since the body is rotating the direction of the position vector is always changing as a result changing the direction of the linear velocity. The direction of linear velocity always acts in the tangential direction of the path.