Question

What is the differential equation of all parabolas whose axis is along the y-axis?
$\left( a \right)x\dfrac{{{d^2}y}}{{d{x^2}}} - \dfrac{{dy}}{{dx}} = 0$
$\left( b \right)x\dfrac{{{d^2}y}}{{d{x^2}}} + \dfrac{{dy}}{{dx}} = 0$
$\left( c \right)\dfrac{{{d^2}y}}{{d{x^2}}} - y = 0$
$\left( d \right)\dfrac{{{d^2}y}}{{d{x^2}}} - \dfrac{{dy}}{{dx}} = 0$

Answer 1

In this particular question consider the standard equation of parabola whose axis is along the y-axis which is given as, ${x^2} = 4ay$, then differentiate this equation w.r.t x, until the constant is eliminated so use these concepts to reach the solution of the question.

Complete step-by-step solution:
__
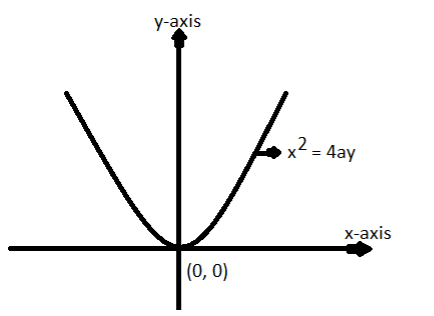
Now,
Consider a standard equation of parabola whose axis is along the y-axis which is given as, ${x^2} = 4ay$ as shown in the above figure.
Now differentiate this equation w.r.t x using the property that $\dfrac{d}{{dx}}{x^n} = n{x^{n - 1}},\dfrac{d}{{dx}}y = \dfrac{{dy}}{{dx}}$ so we have,
$\Rightarrow \dfrac{d}{{dx}}{x^2} = \dfrac{d}{{dx}}\left( {4ay} \right)$
As 4a is constant so it can be written outside the differential operator so we have,
$\Rightarrow \dfrac{d}{{dx}}{x^2} = 4a\dfrac{d}{{dx}}\left( y \right)$
Now differentiate it we have,
$\Rightarrow 2{x^{2 - 1}} = 4a\dfrac{{dy}}{{dx}}$
$\Rightarrow x = 2a\dfrac{{dy}}{{dx}}$................. (1)
Now as we know that in differential equation constant parameters are not present so we have to eliminate them so again differentiate equation (1) w.r.t x until the constant parameter is eliminated so we have,
$\Rightarrow \dfrac{d}{{dx}}x = \dfrac{d}{{dx}}\left( {2a\dfrac{{dy}}{{dx}}} \right)$
Now differentiate it we have,
$\Rightarrow 1 = 2a\dfrac{{{d^2}y}}{{d{x^2}}}$......................... (2)
Now from equation (1) the value of 2a is
$\Rightarrow 2a = \dfrac{x}{{\dfrac{{dy}}{{dx}}}}$
Substitute this value I equation (2) we have,
$\Rightarrow 1 = \dfrac{x}{{\dfrac{{dy}}{{dx}}}}\left( {\dfrac{{{d^2}y}}{{d{x^2}}}} \right)$
Now simplify this we have,
$\Rightarrow \dfrac{{dy}}{{dx}} = x\left( {\dfrac{{{d^2}y}}{{d{x^2}}}} \right)$
$\Rightarrow x\dfrac{{{d^2}y}}{{d{x^2}}} - \dfrac{{dy}}{{dx}} = 0$
So this is the required differential equation.
Hence option (a) is the correct answer.

Note: For such types of questions just keep in mind that the differentiation allows us to find the rate of change of a variable w.r.t another variable. Always recall the basic property of differentiation which is given as $\dfrac{d}{{dx}}{x^n} = n{x^{n - 1}},\dfrac{d}{{dx}}y = \dfrac{{dy}}{{dx}}$. Moreover, a differential equation is an equation that relates one or more functions and their derivatives.