Question

What is the difference between identifying a parabola, ellipse, hyperbola and a circle?

Answer 1

To identify the differences between a circle, ellipse, parabola and hyperbola, we must understand the formation methods of these conic sections. We may also use the general equations of each of these to identify the type. We could also use the different eccentricity values for each of these conic sections to differentiate.

Complete step-by-step solution:
We know that circle, ellipse, parabola and hyperbola, all are parts of a conic section, formed by passing a plane through a double cone in different orientations.
The formation of a circle, is shown in the figure below,

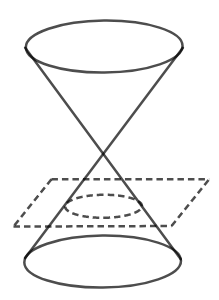
We know that an ellipse is formed when,

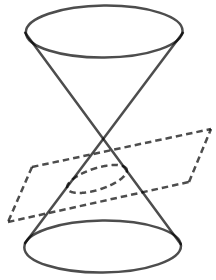
The formation of a parabola is shown in the figure below,

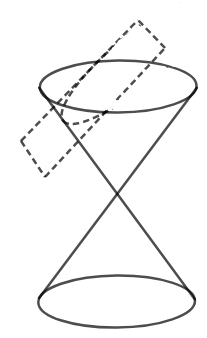
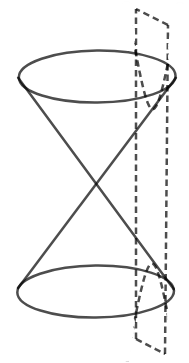
We have also shown the formation of hyperbola through double cone, in the figure below,
Also, we must note the difference in the general equations of each one of these conic sections.
We know that the general equation of a circle is ${{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{r}^{2}}$ .
We also know that the general equation of an ellipse is $\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}+\dfrac{{{\left( y-k \right)}^{2}}}{{{b}^{2}}}=1$ .
We are also aware that the general equation of a parabola is ${{\left( y-k \right)}^{2}}=4a\left( x-h \right)$ .
And, we can write the general equation of a hyperbola as $\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}-\dfrac{{{\left( y-k \right)}^{2}}}{{{b}^{2}}}=1$.

When we need to identify a conic section, these general equations can be our greatest tool.
If the above two methods are not enough for identification, we can use our knowledge of eccentricity to determine the type of conic section.
We know that the eccentricity of a circle is 0.
If the eccentricity is greater than 0 but smaller than 1, then we can say that it is an ellipse.
We know that the eccentricity of a parabola is 1.
And if the eccentricity is greater than 1, then the conic section will be a hyperbola.
Using this information, we can determine whether a given conic section is a circle, ellipse, parabola or a hyperbola.

Note: We must be very clear with these concepts of conic sections. We must also remember the general equations of each type of conic section by heart. We must pay attention that the value of eccentricity is always greater than or equal to zero.