Question

What is the derivative of a whole number, like 1?

Answer 1

First we will understand the meaning of the derivative of a function. In the next step we will check if a particular whole number, like 1, is a constant function or variable function by sketching its graph. If it will be a variable function then we will try to find out the equation of the curve and differentiate it using the basic formulas. If it will be a constant function then its derivative will be 0.

Complete step by step solution:
Here we have been asked to find the derivative of a whole number which we may take as 1. First we need to understand the basic definition of the derivative of a function.
Now, the derivative of a function is defined as the rate of change of function, i.e. change in the value of the function with respect to the variable on which it depends. Derivatives are a fundamental tool of calculus, for example: the derivative of the position of a moving object with respect to time is the object’s velocity, this measures how quickly the position of the object changes when time advances. This derivative is referred to as an instantaneous rate of change.
If we have a function $y=f\left( x \right)$ then its derivative is defined as:
$\Rightarrow \dfrac{dy}{dx}=\displaystyle \lim_{{{x}_{2}} \to {{x}_{1}}}\left[ \dfrac{f\left( {{x}_{2}} \right)-f\left( {{x}_{1}} \right)}{{{x}_{2}}-{{x}_{1}}} \right]$
This change in the value of function is considered for infinitesimally small change in the value of the variable x. From the above formula we can conclude that if we have a constant function then the value of $f\left( x \right)$ will not change for any value of the variable x, that means $f\left( {{x}_{2}} \right)=f\left( {{x}_{1}} \right)$ so the numerator will become zero and hence we will get $\dfrac{dy}{dx}=0$.
Let us come to the question. Here we have a whole number (say 1) as our function.
$\Rightarrow y=f\left( x \right)=1$
Let us sketch its graph.

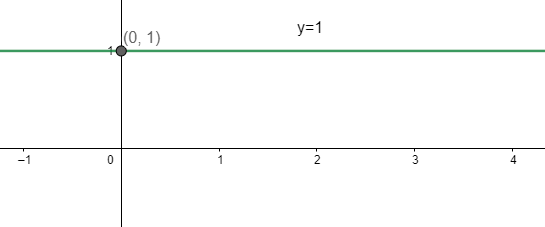
From the above graph we can conclude that the value of $f\left( x \right)$ will remain constant (equal to 1) for all the values of x. That means we have the condition $f\left( {{x}_{2}} \right)=f\left( {{x}_{1}} \right)$ and therefore the derivative will be 0.
$\begin{aligned} & \Rightarrow \dfrac{dy}{dx}=\displaystyle \lim_{{{x}_{2}} \to {{x}_{1}}}\left[ \dfrac{f\left( {{x}_{2}} \right)-f\left( {{x}_{1}} \right)}{{{x}_{2}}-{{x}_{1}}} \right] \\\ & \Rightarrow \dfrac{dy}{dx}=\displaystyle \lim_{{{x}_{2}} \to {{x}_{1}}}\left[ \dfrac{1-1}{{{x}_{2}}-{{x}_{1}}} \right] \\\ & \therefore \dfrac{dy}{dx}=0 \\\ \end{aligned}$
Hence, the derivative of a whole number will be 0.

Note: You may note that for not only 1 but for all the whole numbers or functions which are constant, the derivative is 0. You must remember the basic formula of derivative$\displaystyle \lim_{{{x}_{2}} \to {{x}_{1}}}\left[ \dfrac{f\left( {{x}_{2}} \right)-f\left( {{x}_{1}} \right)}{{{x}_{2}}-{{x}_{1}}} \right]$ also known as the first principle of derivative. All the formulas of differentiation are derived using the first principle. The derivative of a curve at a point is nothing but its slope at that point.