Question

What is the decrease in weight of a body of mass $600{\text{ }}kg$ when it is taken in a mine of depth $5000{\text{ }}m$? [Radius of earth a $6400{\text{ }}km$, $g = 9.8{\text{ }}\dfrac{m}{{{s^2}}}$]

Answer 1

When a body is taken at a depth from the surface of the Earth then the acceleration due to gravity also changes. Hence, we have to find the acceleration due to gravity at that depth. Then, we will find the weight of the body at that height and even get the decreased weight by subtracting it from the weight at the surface.

Complete step by step answer:

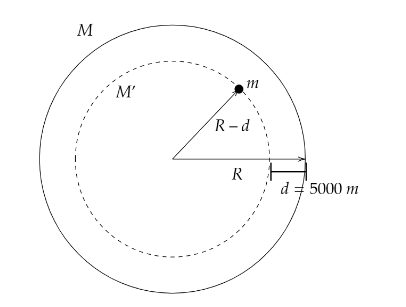
We know that the formula of acceleration due to gravity at the surface of Earth stands as,
$g = \dfrac{{GM}}{{{R^2}}} - - - - \left( 1 \right)$
Where $G =$ Universal Gravitational Constant, $M =$ Mass of the Earth and $R =$ radius of the Earth

If we take the body at a depth $d$ from the surface of the Earth, the mass that it encompasses will be $M'$. Let us consider Earth as spherical.
With mass $M$ the volume that it encloses is $\dfrac{4}{3}\pi {R^3} - - - - \left( 2 \right)$
With mass $M'$ the volume that it encloses is $\dfrac{4}{3}\pi {(R - d)^3} - - - - \left( 3 \right)$
Dividing $\left( 2 \right)$ by $\left( 3 \right)$ we get,
$\dfrac{M}{{M'}} = \dfrac{{\dfrac{4}{3}\pi {R^3}}}{{\dfrac{4}{3}\pi {{(R - d)}^3}}} \\\ \Rightarrow \dfrac{M}{{M'}}= \dfrac{{{R^3}}}{{{{\left( {R - d} \right)}^3}}}$

Hence, we find the relation,
$M' = \dfrac{{{{\left( {R - d} \right)}^3}}}{{{R^3}}} \times M$
By using relation $\left( 1 \right)$ we get the acceleration due to gravity at depth $d$ as,
$g' = \dfrac{{GM'}}{{{{(R - d)}^2}}} \\\ \Rightarrow g' = \dfrac{G}{{{{(R - d)}^2}}} \times \dfrac{{{{\left( {R - d} \right)}^3}}}{{{R^3}}} \times M \\\ \Rightarrow g' = \dfrac{{GM}}{{{R^3}}} \times \left( {R - d} \right)$
Simplifying the equation we get,
$g' = \dfrac{{GM}}{{{R^2}}} \times \left( {1 - \dfrac{d}{R}} \right)$
Substituting the value of $g$ from equation $\left( 1 \right)$ we get,
$g' = g\left( {1 - \dfrac{d}{R}} \right)$

Now, by substituting the values given in the question, we find the weight at a depth $5000{\text{ }}m$,
$mg' = mg\left( {1 - \dfrac{d}{R}} \right) = 600 \times 9.8 \times \left( {1 - \dfrac{{5000}}{{6400000}}} \right) \approx 5875.40{\text{ }}N$
The initial weight at the surface of the Earth is,
$mg = 600 \times 9.8 = 5880{\text{ }}N$
The decreased weight,
$\therefore mg - mg' = 5880 - 5875.40 = 4.6{\text{ }}N$

Hence, the weight decreases by $4.6{\text{ }}N$ when we take the body to a mine of depth $5000{\text{ }}m$.

Note: It must be noted that we must consider the amount of mass of the earth whose radius would be the distance between the centre of the Earth and the position of the body in which it is placed. Weight of a body is the product of the acceleration due to gravity at that place to the mass of the body. Hence, the mass of a body never changes while the weight changes from place to place.