Question

What is the current I shown in the given circuit?

A. $\dfrac{V}{2R}$
B. $\dfrac{V}{R}$
C. $\dfrac{V}{16R}$
D. $\dfrac{V}{8R}$

Answer 1

Recall that a parallel component of a circuit is a current dividing component of the circuit. Using this, determine all the points at which the current gets divided in the circuit and subsequently arrive at the magnitude of current through each of the current dividing branches. Keep in mind that the voltage gets divided in a similar way across series components.
This should finally lead you to the current through the resistor in the last branch in terms of current through the second branch, which you can determine by using Ohm’s law and arrive at the required expression.

Formula used:
Ohm’s Law: $I=\dfrac{V}{R}$

Complete answer:
We begin under the preface that the current gets divided across parallel components of the circuit but remains unchanged for components in series.

The equivalent circuit as the current flows from the voltage source to the resistor across branch BC is shown in the figure below. Thus, the current through the resistor arises due to the resistance of value 2R and is given as $I_1 = \dfrac{V}{2R}$, since the series resistance leaves the current unchanged.

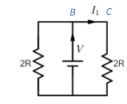
Now, as the current flows through, there is a division of current proportional to the resistance whenever the current encounters a parallel resistance, and there is a division of voltage across series resistance.

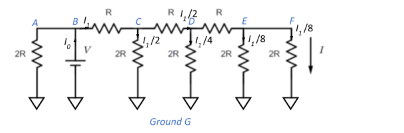
We have $I_1 = \dfrac{V}{2R}$
Therefore, the voltage drop across $R_{BC}$ is
$V_{BC} = I_1 .R_{BC} = \dfrac{V}{2R}.R = \dfrac{V}{2}$
Now, this voltage is established across the resistor $CG$. Therefore, current through $R_{CG}$ is
$I_{CG} = \dfrac{V_{BC}}{R_{CG}} = \dfrac{\dfrac{V}{2}}{2R} = \dfrac{1}{2}\dfrac{V}{2R} = \dfrac{I_1}{2}$
Voltage drop across $R_{CD}$ is
$V_{CD} = I_{CG}.R_{CD} = \dfrac{V}{4R}.R = \dfrac{V}{4}$
Now, this voltage is established across the resistor $DG$. Therefore, current through $R_{DG}$ is
$I_{DG} = \dfrac{V_{CD}}{R_{DG}} = \dfrac{\dfrac{V}{4}}{2R} = \dfrac{1}{4}\dfrac{V}{2R} = \dfrac{I_1}{4}$
Voltage drop across $R_{DE}$ is
$V_{DE} = I_{DG}.R_{RE} = \dfrac{V}{8R}.R = \dfrac{V}{8}$
Now, this voltage is established across the resistor $EG$. Therefore, current through $R_{EG}$ is
$I_{EG} = \dfrac{V_{DE}}{R_{EG}} = \dfrac{\dfrac{V}{8}}{2R} = \dfrac{1}{8}\dfrac{V}{2R} = \dfrac{I_1}{8}$
Since there is no series resistance across EF, the voltage drop across $R_{FG}$ will be $V_{FG} = V_{DE} = \dfrac{V}{8}$
Therefore, the current through $R_{FG}$ will also be $I= I_{FG}= I_{EG} = \dfrac{I_1}{8}$
$\Rightarrow I = \dfrac{V}{2R(8)} = \dfrac{V}{16R}$

So, the correct answer is “Option C”.

Note:
Remember that when a circuit is connected in series, the current flowing through all circuit components will be the same and the voltage drop across each component may be different, whereas, in a parallel circuit, the voltage across the different branches of the circuit will be the same while the current flowing through the branches gets distributed, with the branch of least resistance getting maximum current flow.
Thus, a series circuit is a voltage divider circuit, whereas a parallel circuit is a current divider circuit.