Question

What is the critical value ${{z}_{\dfrac{\alpha }{2}}}$ that corresponds to 93% confidence level?

Answer 1

We must find the value of $\alpha$ according to the given confidence level of 93%. Then, we can use the definition to get the value of $P\left( Z>{{z}_{\dfrac{\alpha }{2}}} \right)$ and thus $P\left( Z<{{z}_{\dfrac{\alpha }{2}}} \right)$. Then, we can use the z-table to find the corresponding z-score.

Complete step-by-step solution:
We know that using 93% confidence level means that 93% of the times a confidence interval is calculated, it will contain the true value of the parameter.
Also, we know very well that $\alpha$ represents the likelihood that the parameter lies outside the confidence interval.
Here, a confidence level of 93% represents the value 0.93 and so, the value of $\alpha$ will be
$\alpha =1-0.93$.
And thus,
$\alpha =0.07$.
So, we can say that $\dfrac{\alpha }{2}=0.035$.
We know that ${{z}_{\dfrac{\alpha }{2}}}$ is the z-score such that the area under the standard normal curve to the right of ${{z}_{\dfrac{\alpha }{2}}}$ is $\dfrac{\alpha }{2}$.
So, we can write $P\left( Z>{{z}_{\dfrac{\alpha }{2}}} \right)=0.035$, and so, $P\left( Z<{{z}_{\dfrac{\alpha }{2}}} \right)=0.965$.

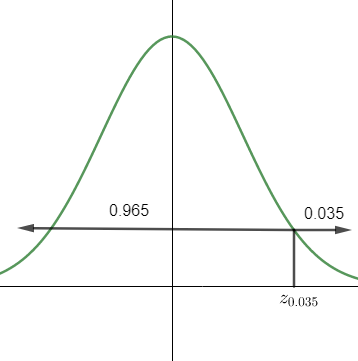
In a z-table having area to the left of z, we must look for the value closest to 0.965 inside the table.

z	.00	.01	.02	.03	.04	.05	.06	.07	.08	.09
1.7	.9554	.9564	.9573	.9582	.9591	.09599	.9608	.9616	.9625	.9633
1.8	.9641	.9649	.9656	.9664	.9671	.9678	.9686	.9693	.9699	.9706
1.9	.9713	.9719	.9726	.9732	.9738	.9744	.9750	.9756	.9761	.9767

We can see that the value closest to 0.965 is 0.9649, which is present along the row 1.8 and column .01.
Thus, the required z-score is 1.81
Hence, the critical value ${{z}_{\dfrac{\alpha }{2}}}$ for 93% confidence level is 1.81

Note: We can also use the linear interpolation technique to solve this problem. The closest value in the z-table, that is, 0.9649 has z-score 1.81 and 0.9656 has z-score 1.82. So, we can now use linear interpolation to find the value of z-score for 0.965 accurately. But, we must understand that this is the approximate answer only.