Question

What is the cosecant and cotangent of $\dfrac{\pi }{3}$ ?

Answer 1

Hint : Here in this question, we have to find the value of trigonometric ratio cosecant and cotangent at an angle of $\dfrac{\pi }{3}$ . This can be found by using the equilateral triangle and Pythagora's identity. And later by using the definition of cosecant and cotangent ratios of trigonometric on simplification, we get the required solution.

Complete step by step solution:

to ${60^ \circ }$ i.e., $\dfrac{\pi }{3} = {60^ \circ }$ .
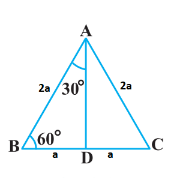
Consider an equilateral triangle ABC. Since each angle in an equilateral triangle is 60°, therefore, $\left| \\!{\underline {\, A \,}} \right. = \left| \\!{\underline {\, B \,}} \right. = \left| \\!{\underline {\, C \,}} \right. = {60^ \circ }$
Draw the perpendicular AD from A to the side BC.
$\therefore \,\,\Delta \,ABD \cong \Delta \,ACD$
$\Delta \,ABD$ is a right triangle, right-angled at D with $\left| \\!{\underline {\, {BAD} \,}} \right. = {30^ \circ }$ and $\left| \\!{\underline {\, {ABD} \,}} \right. = {60^ \circ }$
For finding the trigonometric ratios, we need to know the lengths of the sides of the triangle. So, let us suppose that $AB = AC = BC = 2a$ . Then,
$\Rightarrow \,BD = \dfrac{1}{2}BC$
$\Rightarrow \,BD = \dfrac{1}{2}BC$
$\Rightarrow \,BD = \dfrac{1}{2} \cdot 2a$
$\Rightarrow \,BD = a$
Now, the height of the $\Delta \,ABC$ is AD then by Pythagoras theorem i.e., $A{B^2} = A{D^2} + B{D^2}$ , then
$\Rightarrow \,\,A{D^2} = A{B^2} - B{D^2}$
$\Rightarrow \,\,A{D^2} = {\left( {2a} \right)^2} - {\left( a \right)^2}$
$\Rightarrow \,\,A{D^2} = 4{a^2} - {a^2}$
$\Rightarrow \,\,A{D^2} = 3{a^2}$
$\Rightarrow \,\,AD = \sqrt {3{a^2}}$
On simplification, we get
$\Rightarrow \,\,AD = \sqrt 3 \,a$
In $\Delta \,ABD$ , for the angle $\left| \\!{\underline {\, A \,}} \right. = {60^ \circ } = \dfrac{\pi }{3}$ , side AD is a opposite side, AB is hypotenuse and BD acts as a adjacent side, then
Now, use the definition of trigonometric ratios
Definition of sine ratio at $\left| \\!{\underline {\, A \,}} \right. = {60^ \circ } = \dfrac{\pi }{3}$ is:
$\sin \left( {\dfrac{\pi }{3}} \right) = \dfrac{{Opposite}}{{Hypotenuse}}$
$\Rightarrow \,\sin \left( {\dfrac{\pi }{3}} \right) = \dfrac{{AD}}{{AB}}$
$\Rightarrow \,\sin \left( {\dfrac{\pi }{3}} \right) = \dfrac{{\sqrt 3 a}}{{2a}}$
On simplification, we get
$\Rightarrow \,\sin \left( {\dfrac{\pi }{3}} \right) = \dfrac{{\sqrt 3 }}{2}$
Definition of cosine ratio at $\left| \\!{\underline {\, A \,}} \right. = {60^ \circ } = \dfrac{\pi }{3}$ is:
$\cos \left( {\dfrac{\pi }{3}} \right) = \dfrac{{Adjacent}}{{Hypotenuse}}$
$\Rightarrow \,\cos \left( {\dfrac{\pi }{3}} \right) = \dfrac{{BD}}{{AB}}$
$\Rightarrow \,\cos \left( {\dfrac{\pi }{3}} \right) = \dfrac{a}{{2a}}$
On simplification, we get
$\Rightarrow \,\cos \left( {\dfrac{\pi }{3}} \right) = \dfrac{1}{2}$
As we know, by the definition of trigonometric ratios cosecant is a reciprocal of sine.
Cosecant ratio at $\left| \\!{\underline {\, A \,}} \right. = {60^ \circ } = \dfrac{\pi }{3}$ is:
$\csc \left( {\dfrac{\pi }{3}} \right) = \dfrac{1}{{\sin \left( {\dfrac{\pi }{3}} \right)}}$
On substituting value of $\sin \left( {\dfrac{\pi }{3}} \right)$ , we have
$\Rightarrow \,\,\csc \left( {\dfrac{\pi }{3}} \right) = \dfrac{1}{{\dfrac{{\sqrt 3 }}{2}}}$
On simplification, we get
$\Rightarrow \,\,\csc \left( {\dfrac{\pi }{3}} \right) = \dfrac{2}{{\sqrt 3 }}$
Again, by the definition we know, cotangent is the ratio between the cosine and sine, then
cotangent ratio at $\left| \\!{\underline {\, A \,}} \right. = {60^ \circ } = \dfrac{\pi }{3}$ is:
On substituting value of $\cos \left( {\dfrac{\pi }{3}} \right)$ and $\sin \left( {\dfrac{\pi }{3}} \right)$ , we have
$\Rightarrow \,\,\cot \left( {\dfrac{\pi }{3}} \right) = \dfrac{{\cos \left( {\dfrac{\pi }{3}} \right)}}{{\sin \left( {\dfrac{\pi }{3}} \right)}}$
$\Rightarrow \,\,\cot \left( {\dfrac{\pi }{3}} \right) = \dfrac{{\dfrac{1}{2}}}{{\dfrac{{\sqrt 3 }}{2}}}$
$\Rightarrow \,\,\cot \left( {\dfrac{\pi }{3}} \right) = \dfrac{1}{2} \times \dfrac{2}{{\sqrt 3 }}$
On simplification, we get
$\Rightarrow \,\,\cot \left( {\dfrac{\pi }{3}} \right) = \dfrac{1}{{\sqrt 3 }}$
Hence, the value of $\csc \left( {\dfrac{\pi }{3}} \right) = \dfrac{2}{{\sqrt 3 }}$ and $\cot \left( {\dfrac{\pi }{3}} \right) = \dfrac{1}{{\sqrt 3 }}$
So, the correct answer is “ $\csc \left( {\dfrac{\pi }{3}} \right) = \dfrac{2}{{\sqrt 3 }}$ and $\cot \left( {\dfrac{\pi }{3}} \right) = \dfrac{1}{{\sqrt 3 }}$ ”.

Note : When solving these type of questions, first we have to know the definition of six trigonometric ratios i.e., sine, cosine, tangent, secant, cosecant and cotangent and know the property of equilateral triangle i.e., all sides and angles of equilateral triangle is equal and know the formula of Pythagoras theorem i.e., $hy{p^2} = ad{j^2} + op{p^2}$ .