Question

What is the circum – center of the triangle with coordinates J(1, 3), K(3, -1), M(5, 3)?

Answer 1

Draw a diagram of a triangle JKM inscribed in a circle and assume the center of the circle as O(x, y). Join OJ, OK and OM and assume their length as ${{r}_{1}},{{r}_{2}}$ and ${{r}_{3}}$ respectively. Use the distance formula given as $d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$, where d is the distance between the two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$, to calculate the value of ${{r}_{1}},{{r}_{2}}$ and ${{r}_{3}}$. Now, substitute ${{r}_{1}}={{r}_{3}}$ and find the value of x coordinate. Further, substitute ${{r}_{2}}={{r}_{3}}$ and put the value of x obtained above in the relation to get the value of y coordinate.

Complete step by step solution:
Here we have been provided with a triangle with coordinates J(1, 3), K(3, -1), M(5, 3) and we have to determine the coordinate of the circum – center of this triangle. Let us draw a triangle inscribed in a circle.

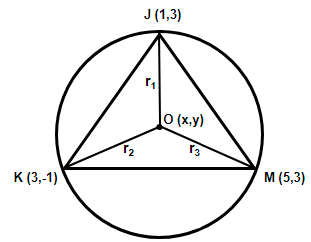
In the above figure we have assumed the center of the circle as O (0, 0). We have joined the points to form the line segments OJ, OK and OM and assumed them as ${{r}_{1}},{{r}_{2}}$ and ${{r}_{3}}$. Using the distance formula given as $d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$, where d is the distance between the two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$, we get,
(1) ${{r}_{1}}=\sqrt{{{\left( x-1 \right)}^{2}}+{{\left( y-3 \right)}^{2}}}$
(2) ${{r}_{2}}=\sqrt{{{\left( x-3 \right)}^{2}}+{{\left( y+1 \right)}^{2}}}$
(3) ${{r}_{3}}=\sqrt{{{\left( x-5 \right)}^{2}}+{{\left( y-3 \right)}^{2}}}$
Now, we can see that ${{r}_{1}},{{r}_{2}}$ and ${{r}_{3}}$ so they must be equal in length, therefore we have the condition ${{r}_{1}}={{r}_{2}}={{r}_{3}}$. Equating ${{r}_{1}}={{r}_{3}}$ we get,
$\Rightarrow \sqrt{{{\left( x-1 \right)}^{2}}+{{\left( y-3 \right)}^{2}}}=\sqrt{{{\left( x-5 \right)}^{2}}+{{\left( y-3 \right)}^{2}}}$
On squaring both the sides we get,
$\Rightarrow {{\left( x-1 \right)}^{2}}+{{\left( y-3 \right)}^{2}}={{\left( x-5 \right)}^{2}}+{{\left( y-3 \right)}^{2}}$
Cancelling the like terms from both the sides we get,

& \Rightarrow {{\left( x-1 \right)}^{2}}={{\left( x-5 \right)}^{2}} \\\ & \Rightarrow {{\left( x-1 \right)}^{2}}-{{\left( x-5 \right)}^{2}}=0 \\\ \end{aligned}$$ Using the algebraic identity ${{a}^{2}}-{{b}^{2}}=\left( a-b \right)\,\left( a+b \right)$ we get, $$\begin{aligned} & \Rightarrow \left( x-1-x+5 \right)\left( x-1+x-5 \right)=0 \\\ & \Rightarrow 4\left( 2x-6 \right)=0 \\\ & \therefore x=3.......\left( i \right) \\\ \end{aligned}$$ Now, equating ${{r}_{2}}={{r}_{3}}$ we get, $$\Rightarrow \sqrt{{{\left( x-3 \right)}^{2}}+{{\left( y+1 \right)}^{2}}}=\sqrt{{{\left( x-5 \right)}^{2}}+{{\left( y-3 \right)}^{2}}}$$ On squaring both the sides we get, $$\Rightarrow {{\left( x-3 \right)}^{2}}+{{\left( y+1 \right)}^{2}}={{\left( x-5 \right)}^{2}}+{{\left( y-3 \right)}^{2}}$$ Substituting the value of x from equation (i) in the above relation we get, $$\begin{aligned} & \Rightarrow {{\left( 3-3 \right)}^{2}}+{{\left( y+1 \right)}^{2}}={{\left( 3-5 \right)}^{2}}+{{\left( y-3 \right)}^{2}} \\\ & \Rightarrow {{\left( y+1 \right)}^{2}}=4+{{\left( y-3 \right)}^{2}} \\\ & \Rightarrow {{\left( y+1 \right)}^{2}}-{{\left( y-3 \right)}^{2}}=4 \\\ \end{aligned}$$ Again using the algebraic identity ${{a}^{2}}-{{b}^{2}}=\left( a-b \right)\,\left( a+b \right)$ we get, $$\begin{aligned} & \Rightarrow \left( y+1-y+3 \right)\left( y+1+y-3 \right)=4 \\\ & \Rightarrow 4\left( 2y-2 \right)=4 \\\ & \therefore y=\dfrac{3}{2} \\\ \end{aligned}$$ **Hence, the coordinate of the circum – center of the triangle is $O\left( 3,\dfrac{3}{2} \right)$.** **Note:** Once the coordinate of the circum – center is found you can easily determine the circum – radius of the circle and its equation. Here you can substitute any of the three radii with each other to get the answer. We have substituted ${{r}_{1}}={{r}_{3}}$ at the first step because we see that the term $${{\left( y-3 \right)}^{2}}$$ will get cancelled on both the sides so we can directly find the value of x without any difficult calculations. Therefore, you need to observe these small things to save time.