Question

What is the centroid of a triangle with vertices at $\left( a,b \right)$, $\left( c,d \right)$ and $\left( e,f \right)$?

Answer 1

We know that the centroid is the intersecting point of its medians. So, first we need to calculate the midpoint of any side. Then, by using the information that the centroid divides the median in the ratio 2 : 1, we can use section formulas to find the coordinates of the centroid.

Complete step-by-step answer:
We know that in a triangle, the line joining any vertex with the midpoint of the opposite side is called a median of that triangle. We also know that all three medians of any triangle are always concurrent, that is, they all intersect at one point. We call this intersection point of all the medians as the centroid of that triangle.
Let us assume a triangle ABC with vertices at A$\left( a,b \right)$, B$\left( c,d \right)$ and C$\left( e,f \right)$.

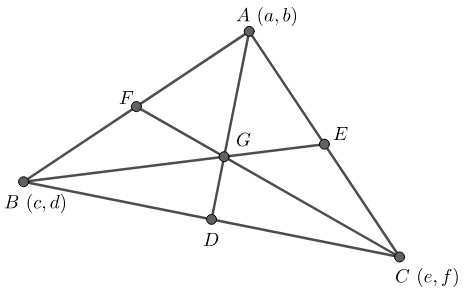
Here, D is the midpoint of BC, E is the midpoint of AC and F is the midpoint of AB.
So, AD, BE and CF are the three medians of this triangle. They intersect at the point G. Thus, the point G is the centroid of our triangle.
We know that for points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$, we can find the mid-point of these points using the mid-point formula, $\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$.
Here, D is the mid-point of B$\left( c,d \right)$ and C$\left( e,f \right)$.
So, the coordinates of point D are $\left( \dfrac{c+e}{2},\dfrac{d+f}{2} \right)$.
We also know that the centroid divides the median in the ratio 2 : 1, that is, $\dfrac{AG}{DG}=\dfrac{2}{1}$.
We know by the section formula, that the coordinates of a point that divides the line segment joining the points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$, in the ratio m : n, is given by $\left( \dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right)$.
Here, the line segment joining the points A$\left( a,b \right)$ and D$\left( \dfrac{c+e}{2},\dfrac{d+f}{2} \right)$ is divided into the ratio 2 : 1, by the point G. Hence, the coordinates of point G will be
$\left( \dfrac{2\left( \dfrac{c+e}{2} \right)+1\left( a \right)}{2+1},\dfrac{2\left( \dfrac{d+f}{2} \right)+1\left( b \right)}{2+1} \right)$.
On simplifying, we can say that coordinates of G are $\left( \dfrac{a+c+e}{3},\dfrac{b+d+f}{3} \right)$.
Hence, the coordinates of the centroid are $\left( \dfrac{a+c+e}{3},\dfrac{b+d+f}{3} \right)$.

Note: We can also solve this problem by finding the coordinates of any two midpoints, and then calculating the equation of those two medians. We can then solve those two equations simultaneously to find their intersecting points. This point will be the centroid of our triangle.