Question

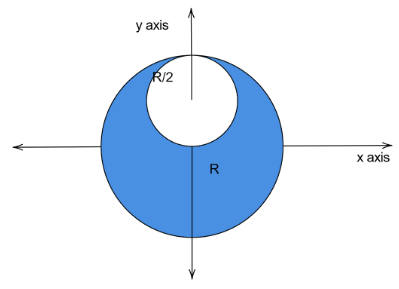
What is the center of mass of the object given below? The object is uniformly dense. All answers are stated with respect to the origin, located at the center of the large sphere.
(a) $\left( {0,\dfrac{R}{2}} \right)$
(b) $\left( {0,\dfrac{R}{4}} \right)$
(c) $\left( {0, - \dfrac{R}{4}} \right)$
(d) $\left( {0, - \dfrac{R}{6}} \right)$
(e) $\left( {0, - \dfrac{R}{3}} \right)$

Answer 1

Hint : We can start by defining the center of mass of an object. Then we move onto the given information, that is, density of the object is given and from this, we find the mass of the object from there, we can find the center of mass using the formula given below.
The formula for the density of an object is given by, $\rho = \dfrac{m}{v}$ where $m$ is the mass of the object and $v$ is the volume of the object.
The formula for area (since this is a two-dimensional object, we use area instead of volume), $A = \pi {r^2}$ , where $r$ is the radius of the circle.

Complete Step By Step Answer:
Let us start by defining the center of mass of an object, it is a point representing the mean position of matter in the object.
Now, analyzing the given object. From the figure, it is clear that the object is two-dimensional. It comprises of two circles, a larger one with radius, $R$ and the smaller one with radius, $r$
We can see that both the circles are symmetrical to the y-axis, hence we conclude that the center of mass lies in the y-axis.
Now let us consider these two circles, one of mass $m$ and the other of mass $m'$ . We can now find a relationship between these masses from density.
The density of the bigger circle is given by, $\rho = \dfrac{m}{{\pi {R^2}}}$
The density of the smaller circle is given by, $\rho = \dfrac{{m'}}{{\pi {{\left( {\dfrac{R}{2}} \right)}^2}}}$
Since it is given that the densities are equal, we equate these two equations to find a relation between the masses
$\dfrac{m}{{\pi {R^2}}} = \dfrac{{m'}}{{\pi {{\left( {\dfrac{R}{2}} \right)}^2}}}$
Cancelling the constants and cross multiplying, we get
$m' = \dfrac{m}{4}$
Considering two circles as point masses and $x = 0$
$y = \dfrac{{m \times 0 - m'R/2}}{{m - m'}} = \dfrac{{ - m' \times R/2}}{{4m' - m'}} = \dfrac{R}{6}$
We already had the value of $x = 0$ and now we have the value of $y = \dfrac{R}{6}$
In conclusion, the center of mass of the given object is at $\left( {0, - \dfrac{R}{6}} \right)$
Option (d) $\left( {0, - \dfrac{R}{6}} \right)$ is the right answer.

Note :
We can see that the object is two-dimensional. Density is the ratio of the mass of the object to its volume, here area is considered instead of volume because it is a two-dimensional object and volume is nothing but the product of area and height.