Question

What is the cartesian form of complex numbers ?

Answer 1

Hint : The cartesian form of a complex number is represented in a two – dimensional plane . Let $a + ib$ be a complex number , here $a$ represents the real part of the complex number and $b$ represents the imaginary part of the complex number .

Complete step-by-step answer :
A complex number system is a form of number system in which imaginary numbers are represented . The cartesian plane of the complex number has two axes - one is the imaginary axis and the other one is the real axis . For better understanding , let us take an example :
Let ${z_1} = a + ib$ be a complex number . Let us plot it on a cartesian plane .

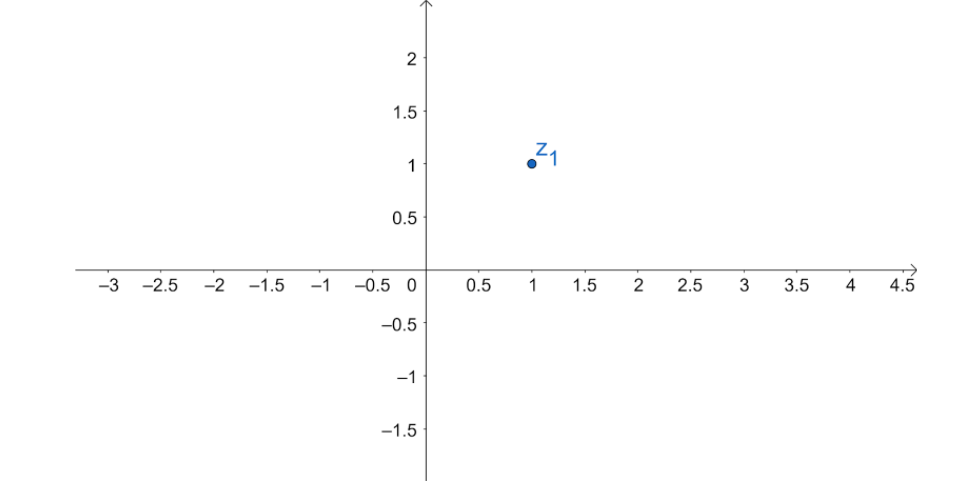
The real number is called the subset of the complex number as when we have $b = 0$ . Also , the conjugate of a complex number can be represented on cartesian plane such as :
${z_2} = \overline {a + ib}$ can be represented as ,

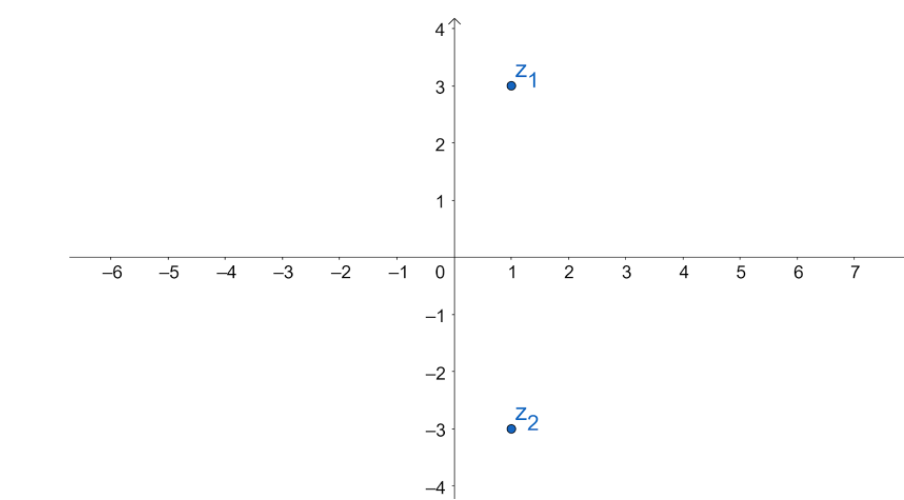
Therefore , the imaginary part will become negative after taking the conjugate of a complex number . A complex number can be represented in a Cartesian axis diagram with a real and an imaginary axis - also known as the Argand diagram .

Note : The argument of a complex number can be calculated by taking $\tan$ of slope of the point . The argument of $\overline {{z_1}}$ depends upon the quadrant in which point ${z_1}$ lies . The conjugate of a complex number is represented by $\overline {{z_1}}$ which is equal to $\overline {{z_1}} = a - ib$ . The plane on which a complex number is represented is also known as the Gaussian plane .