Question

What is the basic difference between the law of Sines and the law of Cosines?

Answer 1

Hint : As we know that sine and cosine both are trigonometric ratios. The law of cosines is generally if at least there elements of the triangle are known to us. When we are given either two angles and one side or two sides and a non included angle, the sine rule is used. When we are given either three sides or two sides and the included angle, the cosine rule is used.

Complete step by step solution:
We know that the cosine rule relates the cosine of an angle of a triangle to the sides of a triangle while the sine rule gives the ratio of the sine of two angles of a triangle which equals the ratio of the corresponding opposite sides.
From the basic concepts of triangles we know when to use the law of cosines and sines.
Let us draw a diagram stating the above:

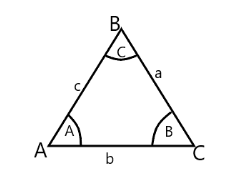
We know that the law of sines establishes a relationship between the angles and side lengths of triangle ABC . So we can write it as $\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}}$ .
While the law of Cosines establishes a relationship between the angles and the side lengths of triangle ABC, so we can write ${c^2} = {a^2} + {b^2} - 2ab\cos C,{a^2} = {b^2} + {c^2} - 2bc\cos A$ and ${b^2} = {a^2} + {c^2} - 2ac\cos B$ .
Hence these are the basic difference between the law of sines and cosines.

Note : We should note that while answering questions of these types we should be sure with the concepts and the formula that we are going to apply. With the help of cosine rule, the angles of a triangle can be determined, if all its sides are known. While with the help of cosine rule we can determine any one of the four elements if other three are known.