Question

What is the axis of symmetry and coordinates of the vertex $y=4{{x}^{2}}-8x-3$?

Answer 1

For solving this question you should know about the general form and to calculate the coordinates of the vertex and the axis of symmetry for any equation. If we compare to the general form with this equation then it is not in a form as the general form. So, first we will change this equation in the general form and then calculate the coordinate of the vertex and axis of symmetry by comparing both.

Complete step by step solution:
According to our question it is asked of us to calculate the coordinate of vertex and the axis of symmetry of $y=4{{x}^{2}}-8x-3$. As we know that the general form for this is, $y=a{{\left( x-h \right)}^{2}}+k$ and here we will get the vertex at $\left( h,k \right)$ which are the coordinates of the vertex. And the axis of symmetry represents $x$. So, if we compare $y=4{{x}^{2}}-8x-3$ with $y=a{{\left( x-h \right)}^{2}}+k$, then we can see that both are not in the same form and if we change $y=4{{x}^{2}}-8x-3$ to the general form, then, it becomes,
$y=4\left( {{x}^{2}}-2x \right)-3$
For making the whole square we will add 0, as a form of $-4+4$, so we get,
$\begin{aligned} & y=4\left( {{x}^{2}}-2x+1 \right)-3-4 \\\ & \Rightarrow y=4{{\left( x-1 \right)}^{2}}-7 \\\ \end{aligned}$
So, it is the general form. If we compare $4{{\left( x-1 \right)}^{2}}-7$ with the general form, $y=a{{\left( x-h \right)}^{2}}+k$, then we get the vertex at $\left( h,k \right)=\left( 1,-7 \right)$. So, the coordinate for the vertex is $\left( 1,-7 \right)$ and the axis of symmetry is $x=1$.

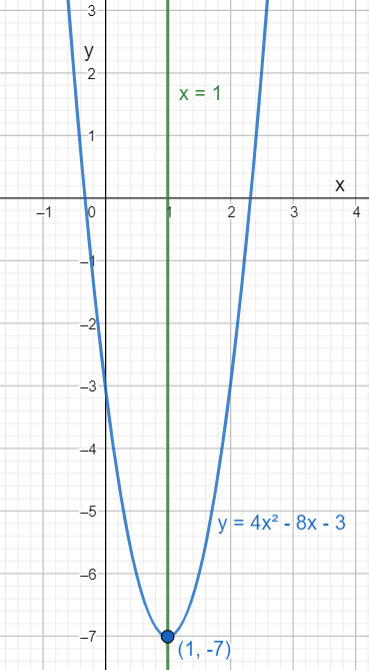
So, the coordinate of the vertex is $\left( 1,-7 \right)$ and the axis of symmetry is $x=1$.

Note: During solving the coordinates of vertex we always have to make sure that the equation which we are comparing with the general form must be in a form of a general equation. And this will give us an exact answer. If both are not in the same form then we will get some other wrong answer.