Question

What is the area of a triangle whose vertices are points with coordinates $\left( 3,2 \right)$ $\left( 5,10 \right)$ and $\left( 8,4 \right)$?

Answer 1

To obtain the area of the triangle we will use coordinate geometry formula. Firstly we will draw a triangle using the given vertices then we will check if it is collinear or not. If it is not collinear we will use the area formula and simplify it to get the desired answer.

Complete step-by-step answer:
The vertices of the triangle are given as:
$\left( 3,2 \right)$ $\left( 5,10 \right)$ $\left( 8,4 \right)$……$\left( 1 \right)$
Now firstly we will plot the vertices and join the points to get the triangle $\Delta ABC$ as:

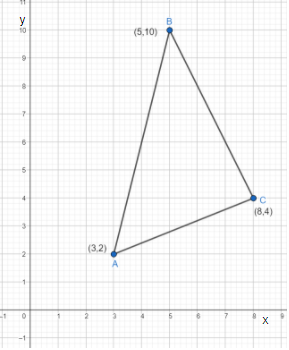
Now we will use the coordinate geometry formula which is:
$A=\dfrac{1}{2}\left| {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right|$…..$\left( 2 \right)$
Where,
$A=$ Area
$\left( {{x}_{1}},{{y}_{1}} \right)\left( {{x}_{2}},{{y}_{2}} \right)\left( {{x}_{3}},{{y}_{3}} \right)$ Are the three vertices of the triangle
On comparing with equation (1) we get the values as:
$\begin{aligned} & {{x}_{1}}=3 \\\ & {{y}_{1}}=2 \\\ & {{x}_{2}}=5 \\\ & {{y}_{2}}=10 \\\ & {{x}_{3}}=8 \\\ & {{y}_{3}}=4 \\\ \end{aligned}$
Substituting above value in equation (2) we get,
$\begin{aligned} & A=\dfrac{1}{2}\left| {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right| \\\ & \Rightarrow A=\dfrac{1}{2}\left| 3\times \left( 10-4 \right)+5\times \left( 4-2 \right)+8\times \left( 2-10 \right) \right| \\\ & \Rightarrow A=\dfrac{1}{2}\left| 3\times 6+5\times 2+8\times \left( -8 \right) \right| \\\ & \Rightarrow A=\dfrac{1}{2}\left| 18+10-64 \right| \\\ \end{aligned}$
On simplifying further we get,
$\begin{aligned} & \Rightarrow A=\dfrac{1}{2}\left| -36 \right| \\\ & \Rightarrow A=\dfrac{36}{2} \\\ & \therefore A=18 \\\ \end{aligned}$
So the Area is 18.
Hence the area of a triangle whose vertices are points with coordinate $\left( 3,2 \right)$ $\left( 5,10 \right)$ and $\left( 8,4 \right)$ is 18.

Note: Triangle is a three edge and three vertices polygon. It is one of the basic shapes used in geometry. The sum of its three angles is always ${{180}^{\circ }}$ and the sum of its two sides is always bigger than the third side. The triangle is denoted by the symbol $\Delta$. There are various types of triangle such as equilateral triangle with all sides equal then there is a right angle triangle whose one angle is always ${{90}^{\circ }}$. Isosceles triangles are those whose w sides are equal and hence two angles are also equal.