Question

What is the area of a square inscribed in a circle of radius 8 cm?
(a) $64c{{m}^{2}}$
(b) $100c{{m}^{2}}$
(c) $125c{{m}^{2}}$
(d) $128c{{m}^{2}}$

Answer 1

Hint: In this question, we will divide the square in two equal triangles with a diagonal, which is also a diameter. We will then use Pythagoras theorem to find the side of the square, and hence area.

Complete step-by-step answer:
Let us consider a square ABCD of radius 8 cm. Let this square ABCD be inscribed by a circle with centre O.
Let us join point A and C of the square to form a diagonal of a square.

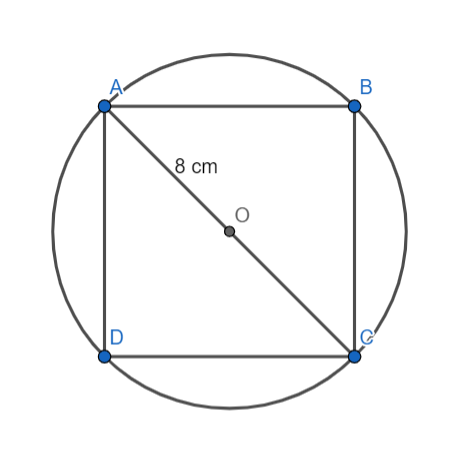
Now, this diagonal AB will pass through the centre of the circle. Also, A and B are the points on the circumference of the circle.
Therefore, AB will be the diameter of the circle.
Since the circle have radius 8 cm,
Therefore,
AC = AO + CO = 8 cm + 8 cm = 16 cm.
Now, we know that all the angles of a square are ${{90}^{\circ }}$. Therefore, here in our diagram, triangle ADC will be a right-angled triangle, right angled at D. So, we can apply Pythagoras theorem here.
Hence, applying Pythagoras theorem in triangle ABC, we have,
$\text{A}{{\text{D}}^{\text{2}}}\text{+D}{{\text{C}}^{\text{2}}}\text{=A}{{\text{C}}^{\text{2}}}$
Also, ABCD is a square and all sides of squares are equal in length. So, let sides of ABCD be $x$.
Therefore, AD = DC = BC = AB = $x$.
Using this and AC = 16 cm, in above equation, we get,
$\begin{aligned} & \text{A}{{\text{D}}^{\text{2}}}\text{+D}{{\text{C}}^{\text{2}}}\text{=A}{{\text{C}}^{\text{2}}} \\\ & \Rightarrow {{x}^{2}}+{{x}^{2}}={{\left( \text{16cm} \right)}^{2}} \\\ & \Rightarrow 2{{x}^{2}}={{16}^{2}}\text{c}{{\text{m}}^{\text{2}}} \\\ & \Rightarrow 2{{x}^{2}}=256\text{c}{{\text{m}}^{\text{2}}} \\\ \end{aligned}$
Diving 2 from both sides of the above equation, we get,
$\begin{aligned} & {{x}^{2}}=\dfrac{256}{2}\text{c}{{\text{m}}^{2}} \\\ & \Rightarrow {{x}^{2}}=128\text{c}{{\text{m}}^{2}} \\\ \end{aligned}$
Also, we know that, area of square is given by,
Area = ${{\left( \text{side} \right)}^{\text{2}}}$.
In square ABCD, side = $x$,
Therefore,
Area of square ABCD $=\,{{x}^{2}}$.
Putting value of ${{x}^{2}}$ here, we get,
Area of square ABCD $=128\text{c}{{\text{m}}^{2}}$ .
Hence the correct answer is option (d).

Note: In this type of question, when value of diagonal of a square is known but sides are not known, then you can directly use the formula: Area of square = $\dfrac{\text{diagona}{{\text{l}}^{\text{2}}}}{\text{2}}$.