Question

What is the area and perimeter of quadrilateral $ABCD$ with vertices $A\left( {6,5} \right),{\text{ }}B\left( {2, - 4} \right),{\text{ }}C\left( { - 5,2} \right)$ and $D\left( { - 3,6} \right)$ ?

Answer 1

In this question, first we will draw a quadrilateral $ABCD$ and then divide the quadrilateral in two triangles (using either of the diagonals). After that we will find the length of the sides of the triangle using distance formula i.e., $d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$ . After that we will find the area of both the triangles using the formula $\sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)}$ where $s = \dfrac{{a + b + c}}{2}$ and $a,b,c$ are the sides of the triangle. Then we will find the area of the quadrilateral by adding the area of the two triangles. We will finally find the perimeter of the given quadrilateral by finding the sum of all its sides.

Complete step by step answer:
Let the vertices of the quadrilateral be $A\left( {6,5} \right),{\text{ }}B\left( {2, - 4} \right),{\text{ }}C\left( { - 5,2} \right)$ and $D\left( { - 3,6} \right)$. Let $AC$ be the diagonal of quadrilateral $ABCD$

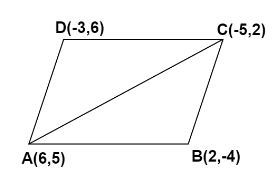
In the above figure, $ABCD$ has been divided into $\vartriangle ABC$ and $\vartriangle ADC$. Now let us find the length of their sides,
Using formula $d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$
Therefore, $AB = \sqrt {{{\left( {2 - 6} \right)}^2} + {{\left( { - 4 - 5} \right)}^2}}$
$\Rightarrow AB = \sqrt {16 + 81} = \sqrt {97} = 9.85$
Similarly,
$BC = \sqrt {{{\left( {2 + 5} \right)}^2} + {{\left( { - 4 - 2} \right)}^2}}$
$\Rightarrow BC = \sqrt {49 + 36} = \sqrt {85} = 9.2$
Similarly,
$AC = \sqrt {{{\left( { - 5 - 6} \right)}^2} + {{\left( {2 - 5} \right)}^2}}$
$\Rightarrow AC = \sqrt {121 + 9} = \sqrt {130} = 11.4$

Similarly,
$AD = \sqrt {{{\left( { - 3 - 6} \right)}^2} + {{\left( {6 - 5} \right)}^2}}$
$\Rightarrow AD = \sqrt {81 + 1} = \sqrt {82} = 9.05$
And
$CD = \sqrt {{{\left( { - 3 + 5} \right)}^2} + {{\left( {6 - 2} \right)}^2}}$
$\Rightarrow CD = \sqrt {4 + 16} = \sqrt {20} = 4.47$
Now we know that
Area of triangle $=$
$\sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)}$ where $s = \dfrac{{a + b + c}}{2}$ and $a,b,c$ are the sides of the triangle.
Thus,
Let triangle be $\vartriangle ABC$ , where $AB = 9.85,{\text{ }}BC = 9.2,{\text{ A}}C = 11.4$
Therefore,
$s = \dfrac{{9.85 + 9.2 + 11.4}}{2}$
$\Rightarrow s = \dfrac{{30.45}}{2} = 15.225$

Now Area of triangle $=$ $\sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)}$
Therefore, area of triangle $\vartriangle ABC$ $= \sqrt {15.225\left( {15.225 - 9.85} \right)\left( {15.225 - 9.2} \right)\left( {15.225 - 11.4} \right)}$
Area of triangle $\vartriangle ABC = \sqrt {15.225\left( {5.375} \right)\left( {6.025} \right)\left( {3.825} \right)}$
On solving, we get
Area of triangle $\vartriangle ABC = \sqrt {1885.92} = 43.4$
Now let triangle be $\vartriangle ADC$ , where $AD = 9.05,{\text{ }}CD = 4.47,{\text{ A}}C = 11.4$
Therefore,
$s = \dfrac{{9.05 + 4.47 + 11.4}}{2}$
$\Rightarrow s = \dfrac{{24.92}}{2} = 12.46$

Now Area of triangle $=$ $\sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)}$
Therefore, area of triangle $\vartriangle ADC$ $= \sqrt {12.46\left( {12.46 - 9.05} \right)\left( {12.46 - 4.47} \right)\left( {12.46 - 11.4} \right)}$
Area of triangle $\vartriangle ADC = \sqrt {12.46\left( {3.41} \right)\left( {7.99} \right)\left( {1.06} \right)}$
On solving, we get
Area of triangle $\vartriangle ADC = \sqrt {359.85} = 18.96$
Hence, the area of quadrilateral $ABCD$ $=$ Area of $\vartriangle ABC$ $+$ Area of $\vartriangle ADC$
area of quadrilateral $ABCD$ $= 43.4 + 18.96$
$\Rightarrow$ area of quadrilateral $ABCD$ $= 62.36$
Now we know that the perimeter of the quadrilateral is the sum of all the sides of the quadrilateral i.e., perimeter of quadrilateral $ABCD$ $= AB + BC + CD + AD$
We have all the values, so we get the perimeter as
$\left( {9.85 + 9.2 + 4.47 + 9.05} \right) = 32.57$

Hence, we get the area of the quadrilateral as $62.36{\text{ }}sq.units$ and the perimeter as $32.57\,units$.

Note: In this type of question, sometimes it's difficult to solve the area of the triangles as the calculation is complex, so, there is one other formula to find the area of the triangle.
$Area = \dfrac{1}{2}|\left[ {{x_1}\left( {{y_2} - {y_3}} \right) + {x_2}\left( {{y_3} - {y_1}} \right) + {x_3}\left( {{y_1} - {y_2}} \right)} \right]$
where $\left( {{x_1},{y_1}} \right),\left( {{x_2},{y_2}} \right),\left( {{x_3},{y_3}} \right)$ are the coordinates of the triangle. Also remember while solving this type of problem, always try to find the area of the quadrilateral by dividing it into two triangles by joining any one of the diagonals. Also try to avoid calculation mistakes.