Question

What is the angle between electron groups in tetrahedral geometry?

Answer 1

The Lewis electron dot structure must be understood in order to identify the shapes of molecules. Although the Lewis theory does not define molecular forms, it is the first step toward predicting molecule shapes. The Lewis structure aids in the identification of bond pairs and lone pairs. The molecular geometry and electron-group geometry are then determined using the valence-shell electron-pair repulsion (VSEPR) theory and the Lewis structure.

Complete answer:
A central atom is placed in the middle of a tetrahedral molecular geometry, with four substituents located at the corners of the tetrahedron. When all four substituents are the same, as in methane ($C{{H}_{4}}$) and its heavier equivalents, the bond angles are $co{{s}^{-1}}\left( \dfrac{-1}{3} \right)\text{ }=\text{ }109.4712206...{}^\circ \text{ }\approx \text{ }109.5{}^\circ$. Point group ${{T}_{d}}$ includes methane and other fully symmetrical tetrahedral molecules, although most tetrahedral molecules have lesser symmetry. Chiral tetrahedral molecules are possible.

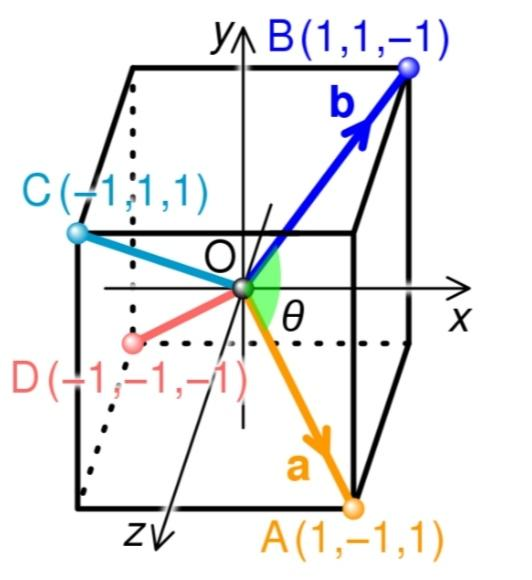
The dot product of two vectors may be used to compute the bond angle of a symmetric tetrahedral molecule like methane. The molecule can be inscribed in a cube as indicated in the picture, with the tetravalent atom (e.g. carbon) at the cube centre, which is the origin of coordinates, O. The four monovalent atoms (e.g. hydrogens) are positioned at the cube's four corners (A, B, C, D), so that no two atoms are connected by a single cube edge. If the cube's edge length is set to two units, the two bonds OA and OB correspond to the vectors a = (1, –1, 1) and b = (1, 1, –1), respectively, and the bond angle $\theta$ is the angle formed by these two vectors.
$a\,\bullet \,b=\text{ }\left| \left| a \right| \right|\text{ }\left| \left| b \right| \right|\text{ }cos\,\theta$

$=\dfrac{\left( \begin{matrix} 1 \\\ \begin{matrix} -1 \\\ 1 \\\ \end{matrix} \\\ \end{matrix} \right)\cdot \left( \begin{matrix} 1 \\\ 1 \\\ -1 \\\ \end{matrix} \right)}{\sqrt{{{1}^{2}}+{{1}^{2}}+{{1}^{2}}}\cdot \sqrt{{{1}^{2}}+{{1}^{2}}+{{1}^{2}}}}$
$=\dfrac{1\times 1+(-1)\times 1+1\times (-1)}{\sqrt{3}\cdot \sqrt{3}}$
$=-\dfrac{1}{3}\theta \text{ }=\arccos \left( -\dfrac{1}{3} \right)\approx {{109.47}^{{}^\circ }}$
The dot product of the two vectors, $a\,\bullet \,b=\text{ }\left| \left| a \right| \right|\text{ }\left| \left| b \right| \right|\text{ }cos\,\theta$ , can be used to compute this angle, where $\left| \left| a \right| \right|$ denotes the length of vector a. The dot product is –1 and the length of each vector is $\sqrt{3}$, as indicated in the picture, thus $cos\,\theta \text{ }=\text{ }\dfrac{-1}{3}$ and the tetrahedral bond angle $arccos\left( \dfrac{1}{3} \right)\text{ }\simeq \text{ }109.47{}^\circ .\text{ }$

Note:
The three-dimensional arrangement of the atoms that make up a molecule is known as molecular geometry. It comprises the molecule's overall form, as well as bond lengths, bond angles, torsional angles, and any other geometrical factors that define each atom's location. The reactivity, polarity, phase of matter, colour, magnetism, and biological activity of a material are all influenced by molecular geometry. The angles between bonds formed by one atom are only weakly dependent on the rest of the molecule, thus they may be thought of as roughly local and hence transferrable characteristics.