Question

What is the ammeter reading?

A. $0.4$
B. $1$
C. $0.6$
D. $1.2$

Answer 1

In the given question first of all we have to find the total resistance in both the upper and lower linear circuits. As the connections are in parallel, we have to find the ratio of resistance in each linear circuit to the total resistance to find the answer.

Complete step by step answer:

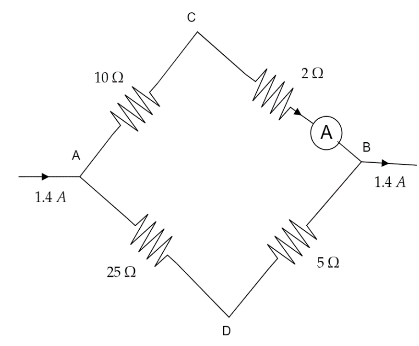
First of all, let us consider the upper linear circuit ACB and its resistance as ${R_1}$.The resistance in the circuit is in series. Hence, the total series combination of the circuit ACB$= \left( {10 + 2} \right) = 12{\text{ }}\Omega$
${R_1} = 12{\text{ }}\Omega$
Now, the circuit ADB is also a series combination of circuit and its resistance is ${R_2}$.
Hence the total resistance of the circuit is $\left( {25 + 5} \right) = 30{\text{ }}\Omega$
${R_2} = 30{\text{ }}\Omega$
The total current in the circuit is given $1.4{\text{ }}A$. Let the current flowing in the circuit ACB be ${i_1}$and the current flowing in circuit ADB be $\left( {1.4 - {i_1}} \right)$.

As the circuits are in parallel combination then, the linear circuits ACB and ADB will get equal amounts of voltage. Let the voltage in the circuit be $V$.From Kirchhoff’s Law of Voltage in circuit ACB we get,
$V = 30i - - - - - \left( 1 \right)$
From Kirchhoff’s Law of Voltage in circuit ADB we get,
$V = 12\left( {1.4 - {i_1}} \right) - - - - - \left( 2 \right)$
From equation $\left( 1 \right)$ and $\left( 2 \right)$ we get,
$30{i_1} = 12\left( {1.4 - {i_1}} \right)$
Simplifying the equation we get,
$30{i_1} + 12{i_1} = 16.8$
$\Rightarrow {i_i} = 0.4$
So, the current flowing in circuit ADB is $0.4{\text{ }}A$.
Now, the current in circuit ACB is $\left( {1.4 - 0.4} \right) = 1{\text{ }}A$.
Hence, we get the ammeter reading as $1{\text{ }}A$.

Hence, the correct option is B.

Note: It must be noted that when circuits are connected in parallel combination the voltage in those circuits remains the same while the current changes. Again, when the circuits are in series combination, then the same amount of current flows through the circuits whereas the voltage is differentiable.