Question

What is the activation energy for a reaction if its rate doubles when the temperature is raised from 20°C to 35°C? ($R = 8.314 \text{Jmol}^{-1}\text{K}^{-1} \log 2 = 0.3010$)

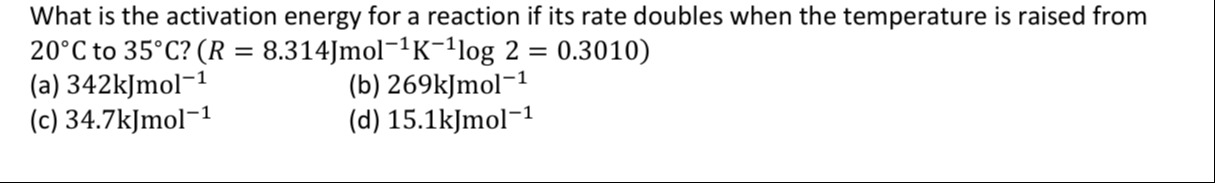
• A. 342kJmol$^{-1}$
• B. 269kJmol$^{-1}$
• C. 34.7kJmol$^{-1}$
• D. 15.1kJmol$^{-1}$

Answer 1

Answer: (C)

The correct answer is 34.7kJmol$^{-1}$

Answer 2

The relationship between the rate constant ($k$) and temperature ($T$) is given by the Arrhenius equation. For two different temperatures $T_1$ and $T_2$, the rate constants $k_1$ and $k_2$ are related by the integrated Arrhenius equation:

$$\ln\left(\frac{k_2}{k_1}\right) = \frac{E_a}{R}\left(\frac{1}{T_1} - \frac{1}{T_2}\right) = \frac{E_a}{R}\left(\frac{T_2 - T_1}{T_1 T_2}\right)$$

where $E_a$ is the activation energy and $R$ is the ideal gas constant.

Given:

$T_1 = 20^\circ\text{C}$ $T_2 = 35^\circ\text{C}$

The rate doubles when the temperature is raised from 20°C to 35°C, which means $k_2 = 2k_1$, so $\frac{k_2}{k_1} = 2$.

$R = 8.314 \text{ Jmol}^{-1}\text{K}^{-1}$ $\log 2 = 0.3010$

First, convert the temperatures from Celsius to Kelvin:

$T_1 = 20 + 273.15 = 293.15 \text{ K}$ $T_2 = 35 + 273.15 = 308.15 \text{ K}$

Now, calculate $\ln\left(\frac{k_2}{k_1}\right)$:

$\ln\left(\frac{k_2}{k_1}\right) = \ln(2)$

Using the relationship $\ln(x) = 2.303 \log_{10}(x)$:

$\ln(2) = 2.303 \times \log_{10}(2) = 2.303 \times 0.3010 = 0.693023$

Now, calculate the temperature difference and the product of temperatures:

$T_2 - T_1 = 308.15 - 293.15 = 15 \text{ K}$ $T_1 T_2 = 293.15 \times 308.15 = 90400.9725 \text{ K}^2$

Substitute these values into the integrated Arrhenius equation:

$$0.693023 = \frac{E_a}{8.314 \text{ Jmol}^{-1}\text{K}^{-1}}\left(\frac{15 \text{ K}}{90400.9725 \text{ K}^2}\right)$$ $$0.693023 = \frac{E_a}{8.314} \times \frac{15}{90400.9725}$$

Solve for $E_a$:

$$E_a = 0.693023 \times 8.314 \times \frac{90400.9725}{15}$$ $$E_a = 0.693023 \times 8.314 \times 6026.7315$$ $$E_a \approx 5.7603 \times 6026.7315$$ $$E_a \approx 34724.8 \text{ J/mol}$$

To convert the activation energy from joules per mole to kilojoules per mole, divide by 1000:

$$E_a \approx \frac{34724.8}{1000} \text{ kJ/mol}$$ $$E_a \approx 34.7248 \text{ kJ/mol}$$

This value is closest to 34.7 kJ/mol.