Question
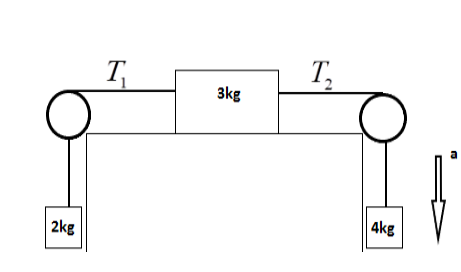
Question: What is the acceleration \( a \) and the tension \( {T_1} \) and \( {T_2} \) in the given system? ...
What is the acceleration a and the tension T1 and T2 in the given system?
Solution
Hint : In this question, we need to evaluate the tension in the wires and the acceleration of the block. For this, we will first make the free body diagrams of the blocks and then, use Newton’s third law equation for this question.
Complete Step By Step Answer:
There is no mention of friction coefficient here. Thus all surfaces are frictionless.
Since the strings are ideal, all the blocks have the same magnitude of acceleration though directions are different for different blocks.
The mass of the right block is more than the left block. Thus the right block will come down.
The respective equations of the blocks are as follows
4g−T1=4a ⇒T1−T2=3a ⇒T2−2g=2a
Adding all equations we get
4g−2g=9a ⇒2g=9a ⇒a=92g ⇒a=2.22ms−2
For the value of T1 we use the equation 4g−T1=4a
Thus,
T1=4g−4a ⇒T1=40−8.88 ⇒T1=31.12N
Again for T2 the value of it can be found by using the equation T2−2g=2a
Thus,
T2=2a+2g ⇒T2=2×2.22+20 ⇒T2=24.44N
Hence, the required answers are a=2.22ms−2 , T1=31.12N and T2=24.44N
Additional Information:
The law used here is Newton’s third law which states that the force is directly proportional to the change in momentum. Here the mathematical expression for this law is given by F=ma . This law is very useful in solving such types of questions.
Note :
The pulley used here is an ideal pulley and hence there is no friction in the rim and the pulley is massless. There are many arrangements of these types using multiple pulleys and surfaces in which friction may be used. Thus, students should be very skeptical about it and have a good amount of knowledge and practice while solving such questions.
