Question

What is $\sin \theta$ and $\cos \theta$ if $\tan \theta = \dfrac{1}{2}$ and $\sin \theta > 0$ ?

Answer 1

Hint : We have to find $\sin \theta$ and $\cos \theta$ . Now, we know that $\tan \theta = \dfrac{{\sin \theta }}{{\cos \theta }}$ , so we can write $\dfrac{{\sin \theta }}{{\cos \theta }} = \dfrac{1}{2}$ . On simplifying it we will get $\cos \theta = 2\sin \theta$ . We know the formula ${\sin ^2}\theta + {\cos ^2}\theta = 1$ and we have the value for $\cos \theta$ . So, substitute the value of $\cos \theta$ and find the value of $\sin \theta$ . After finding the value of $\sin \theta$ , put it in equation $\cos \theta = 2\sin \theta$ and you will get the value of $\cos \theta$ as well.
Formulas used:
$\Rightarrow \tan \theta = \dfrac{{\sin \theta }}{{\cos \theta }}$
$\Rightarrow {\sin ^2}\theta + {\cos ^2}\theta = 1$
$\Rightarrow \tan = \dfrac{{{\text{Opposite}}}}{{Adjacent}} = \dfrac{1}{2}$
$\Rightarrow \sin \theta = \dfrac{{{\text{Opposite}}}}{{{\text{Hypotenuse}}}}$
$\Rightarrow \cos \theta = \dfrac{{Adjacent}}{{{\text{Hypotenuse}}}}$

Complete step-by-step answer :
In this question, we are given the value of $\tan \theta$ and we need to find the values of $\sin \theta$ and $\cos \theta$ .
$\Rightarrow \tan \theta = \dfrac{1}{2}$ and $\sin \theta > 0$ - - - - - - - - - - (1)
Now, we know that $\tan \theta$ is $\sin \theta$ divided by $\cos \theta$ . So, we can write equation (1) as $\sin \theta$ divided by $\cos \theta$ equal to $\dfrac{1}{2}$ . Therefore, equation (1) becomes
$\Rightarrow \dfrac{{\sin \theta }}{{\cos \theta }} = \dfrac{1}{2}$
Cross multiply, we get
$\Rightarrow \cos \theta = 2\sin \theta$ - - - - - - - - - - (2)
Now, we know that the square of $\sin \theta$ plus the square of $\cos \theta$ is always equal to 1.
Therefore, ${\sin ^2}\theta + {\cos ^2}\theta = 1$ - - - - - - - - - (3)
Now, from equation (2) substitute $\cos \theta = 2\sin \theta$ in equation (3). Therefore, we get
$\Rightarrow {\sin ^2}\theta + {\left( {2\sin \theta } \right)^2} = 1$
Open the bracket, we get
$\Rightarrow {\sin ^2}\theta + 4{\sin ^2}\theta = 1 \\\ \Rightarrow 5{\sin ^2}\theta = 1 \\\ \Rightarrow {\sin ^2}\theta = \dfrac{1}{5} \;$
Taking square root on both sides, we get
$\Rightarrow \sin \theta = \pm \sqrt {\dfrac{1}{5}}$
But, according to equation (1), $\sin \theta > 0$ . Hence, the value of $\sin \theta$ cannot be negative.
$\Rightarrow \sin \theta = \sqrt {\dfrac{1}{5}} = \dfrac{1}{{\sqrt 5 }}$
Rationalizing the above equation, we get
$\Rightarrow \sin \theta = \dfrac{1}{{\sqrt 5 }} \times \dfrac{{\sqrt 5 }}{{\sqrt 5 }} = \dfrac{{\sqrt 5 }}{5}$
Now, from equation (2),
$\Rightarrow \cos \theta = 2\sin \theta$
Therefore, $\cos \theta = 2 \times \dfrac{{\sqrt 5 }}{5}$
$\Rightarrow \cos \theta = \dfrac{{2\sqrt 5 }}{5}$
Hence, we have got the values of $\sin \theta$ and $\cos \theta$ .

Note : Alternate method to solve this question is by drawing the triangle.
We know that $\tan = \dfrac{{{\text{Opposite}}}}{{Adjacent}} = \dfrac{1}{2}$

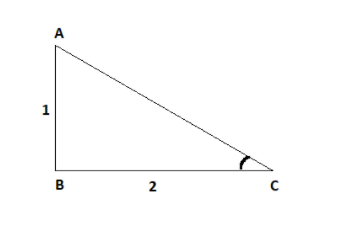
Now, in right angled triangle $ABC$ , using Pythagoras
$\Rightarrow A{B^2} + B{C^2} = A{C^2} \\\ \Rightarrow {1^2} + {2^2} = A{C^2} \\\ \Rightarrow A{C^2} = 5 \\\ \Rightarrow AC = \pm \sqrt 5 \;$
Now, we know that
$\Rightarrow \sin \theta = \dfrac{{{\text{Opposite}}}}{{{\text{Hypotenuse}}}} = \dfrac{{AB}}{{AC}} \\\ \Rightarrow \sin \theta = \dfrac{1}{{\sqrt 5 }} \;$
As $\sin \theta > 0$ .
And, the formula for $\cos \theta$ is
$\Rightarrow \cos \theta = \dfrac{{Adjacent}}{{{\text{Hypotenuse}}}} = \dfrac{{BC}}{{AC}} \\\ \Rightarrow \cos \theta = \dfrac{2}{{\sqrt 5 }} \;$