Solveeit Logo
Login

Question

Question: What is \(\sin \left( \dfrac{\theta }{2} \right)\) in terms of trigonometric functions of a unit \(\...

What is sin⁡(θ2)\sin \left( \dfrac{\theta }{2} \right) in terms of trigonometric functions of a unit θ\theta ?

Explanation

Solution

We first draw a right-angle triangle. We use the concept of trigonometry to find the value as cos⁡θ=ABBC\cos \theta =\dfrac{AB}{BC}. We use the formula of cos⁡θ=1−2sin⁡2(θ2)\cos \theta =1-2{{\sin }^{2}}\left( \dfrac{\theta }{2} \right) to simplify the problem.
We put the values to find the solution with respect to the value of cos⁡θ=m\cos \theta =m.

Complete step-by-step solution:
The expression of sin⁡(θ2)\sin \left( \dfrac{\theta }{2} \right) is the formula of submultiple angles.
We have to explain the significance of the trigonometric values.
Let us assume for ΔABC\Delta ABC, ∠A=90∘\angle A={{90}^{\circ }}.

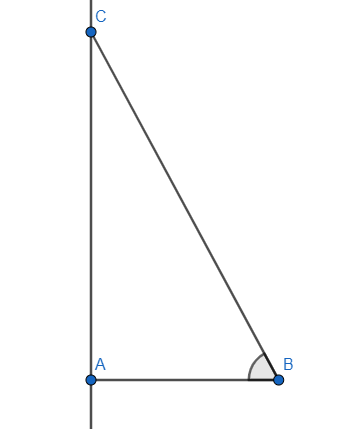
Now let us take ∠B=θ\angle B=\theta .
We know the trigonometric ratio of cos gives the ratio of base and the hypotenuse.
Therefore, cos⁡θ=ABBC\cos \theta =\dfrac{AB}{BC}.
We will use the concept of submultiple to find the value of sin⁡(θ2)\sin \left( \dfrac{\theta }{2} \right).
We have the relation between sin⁡(θ2)\sin \left( \dfrac{\theta }{2} \right) and cos⁡θ\cos \theta which gives cos⁡θ=1−2sin⁡2(θ2)\cos \theta =1-2{{\sin }^{2}}\left( \dfrac{\theta }{2} \right).
Let us assume that cos⁡θ=m\cos \theta =m.
We get 1−2sin⁡2(θ2)=m1-2{{\sin }^{2}}\left( \dfrac{\theta }{2} \right)=m.
From the relation we find the value of sin⁡(θ2)\sin \left( \dfrac{\theta }{2} \right).
We get 2sin⁡2(θ2)=1−m2{{\sin }^{2}}\left( \dfrac{\theta }{2} \right)=1-m which gives
2sin⁡2(θ2)=1−m ⇒[sin⁡(θ2)]2=1−m2 \begin{aligned} & 2{{\sin }^{2}}\left( \dfrac{\theta }{2} \right)=1-m \\\ & \Rightarrow {{\left[ \sin \left( \dfrac{\theta }{2} \right) \right]}^{2}}=\dfrac{1-m}{2} \\\ \end{aligned}
Now we omit the root square part to find the value of sin⁡(θ2)\sin \left( \dfrac{\theta }{2} \right).
So, [sin⁡(θ2)]2=1−m2⇒sin⁡(θ2)=±1−m2{{\left[ \sin \left( \dfrac{\theta }{2} \right) \right]}^{2}}=\dfrac{1-m}{2}\Rightarrow \sin \left( \dfrac{\theta }{2} \right)=\pm \sqrt{\dfrac{1-m}{2}}.
The value of the trigonometric function sin⁡(θ2)\sin \left( \dfrac{\theta }{2} \right) is ±1−m2\pm \sqrt{\dfrac{1-m}{2}} where cos⁡θ=m\cos \theta =m.

Note: We first need to find the relation where we have all the variables given. The use of the relation sin⁡θ=2sin⁡(θ2)cos⁡(θ2)\sin \theta =2\sin \left( \dfrac{\theta }{2} \right)\cos \left( \dfrac{\theta }{2} \right) also gives the same result. In this case we find two ratio values to get to the required solution.