Question

What is refraction of light? How is it related to the refractive index?

Answer 1

The phenomenon of bending of light when it passes through different mediums is called refraction. Refractive index of light travelling with speed v in a medium is given by $\mu =\dfrac{c}{v}$.

Complete step-by-step answer :
Speed of light is different in different mediums. If a ray of light passes from one medium to another, the speed of light changes. The medium in which the speed of light is faster is called the rarer medium and the medium in which the speed of light is slower is called denser medium. When the speed of light changes, it also changes its direction and the light appears to be bending at the interface of the mediums. This bending of light is called refraction.

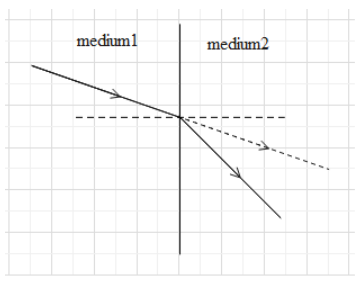
To understand the speed of light in a medium, we have something known as a refractive index. Refractive index ($\mu$) of a medium is that characteristic which decides the speed of light. It is defined as the ratio of the speed of light in vacuum (c) to the speed of light (v) in the given medium i.e. $\mu =\dfrac{c}{v}$.
To compare the refractive indices of different mediums we have a refractive index. When light travels from medium (1) to medium (2) then refractive index of medium (2) with respect to medium (1) is called its relative refractive index and is written as ${}_{1}{{\mu }_{2}}$.
${}_{1}{{\mu }_{2}}=\dfrac{{{\mu }_{2}}}{{{\mu }_{1}}}=\dfrac{\dfrac{c}{{{v}_{2}}}}{\dfrac{c}{{{v}_{1}}}}=\dfrac{{{v}_{1}}}{{{v}_{2}}}$ ……….(1)
If ${}_{1}{{\mu }_{2}}$ is the relative refractive index of medium (2) w.r.t medium (1). Then ${}_{2}{{\mu }_{1}}$ is the relative refractive index of medium (1) w.r.t medium (2).
Therefore,
${}_{2}{{\mu }_{1}}=\dfrac{{{\mu }_{1}}}{{{\mu }_{2}}}=\dfrac{\dfrac{c}{{{v}_{1}}}}{\dfrac{c}{{{v}_{2}}}}=\dfrac{{{v}_{2}}}{{{v}_{1}}}$ ……..(2)
Multiply the equations (1) and (2).
We get, ${}_{1}{{\mu }_{2}}.{}_{2}{{\mu }_{1}}=\dfrac{{{v}_{1}}}{{{v}_{2}}}.\dfrac{{{v}_{2}}}{{{v}_{1}}}=1$
$\Rightarrow {}_{1}{{\mu }_{2}}=\dfrac{1}{{}_{2}{{\mu }_{1}}}$
Therefore, if the refractive index of water with respect to air is 1.33, then the refractive index of air with respect to water will be $\dfrac{1}{1.33}=0.75$.

Note : It can easily be mistaken between ${}_{1}{{\mu }_{2}}$ and ${}_{2}{{\mu }_{1}}$. Therefore, it is necessary to remember that ${}_{1}{{\mu }_{2}}$ is the refractive index of medium (2) with respect to the refractive index of medium (1) and not the converse.