Question

What is potential energy? Derive an equation for the gravitational potential energy of a body mass ‘m’ at a height of ‘h’.

Answer 1

Use the formula of work done. Work done is nothing but change in potential energy. To calculate the value of potential energy, use the formula of force between two bodies. If the position of body changes, on account of force acting on it then potential energy at that position will also change. Change in energy leads to work being done in that position.

Complete step by step solution:
The force of gravity is a conservation force and we can calculate the potential energy of a body arising out of this force called the gravitational potential energy.

Diagram:

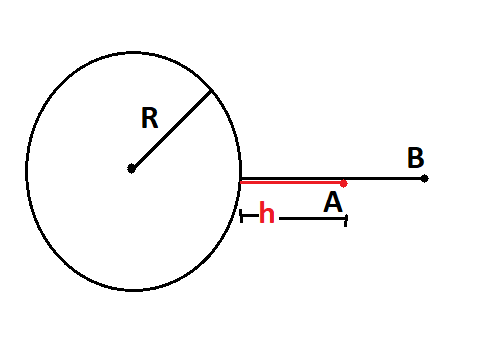
In this diagram our body of mass is at A and B is the arbitrary point which is at infinity. R is the radius of the earth.
An arbitrary body of mass m which is at height of h above the earth. Mass of the earth is M and the radius of earth is R.

Aim: Calculate gravitational energy of the body above earth at a height h.
Let’s consider an earth having mass M. Consider a body of mass m above the earth at a point A of height h. Now consider an arbitrary point B what is at infinity.
Now we know that force by earth on body which is above height h is,
$F=\dfrac{-GMm}{{{r}^{2}}}$
Where,
F = force on body m
G = gravitational energy
M= mass of earth
M = mass of body
R = distance from the centre of earth.
Consider the initial position of the body is at B a final position is at A.
Work done to bring this from B to A is,
Work done = change in P.E.
$\begin{aligned} & F.dr=dw \\\ & \text{therefore},dw=\dfrac{-GMm}{{{r}^{2}}}(-dr) \\\ \end{aligned}$
Negative sign indicates that force is toward the earth due to gravitational force
$w=\int{dw=\int\limits_{\infty }^{h}{\dfrac{GMmdr}{{{r}^{2}}}}}$
Limits on integration indicates that our body has initial position B and final position is A.

**Therefore potential energy is given by,
$\begin{aligned} & P.E=\left[ \dfrac{-GMm}{r} \right]_{\infty }^{h} \\\ & P.E=[\dfrac{-GMm}{R+h}-0] \\\ & \text{potential energy}=\dfrac{-GMm}{R+h} \\\ \end{aligned}$
Gravitational potential energy of a body mass ‘m’ at a height of ‘h’ is $\dfrac{-GMm}{R+h}$.

**

Note: Notice that height of the body is from the surface of earth not from the centre of the earth. Adding height from its centre on height h will give R- H, if H is the height from centre of the earth to the surface of the earth only. In this question, B is just an arbitrary point in space which is at infinity.