Question

What is polarization of light? Explain polarization of light with the suitable diagram and hence derive Brewster’s law.

Answer 1

Brewster’s law states that when light from a medium enters a medium of another medium such that the refractive index one is different from another, it gets polarized. This results in production of two rays i.e. refracted ray and reflected ray which are perpendicular to each other. This occurs when angle of incidence has a certain value called the Brewster’s angle.

Complete step by step solution:

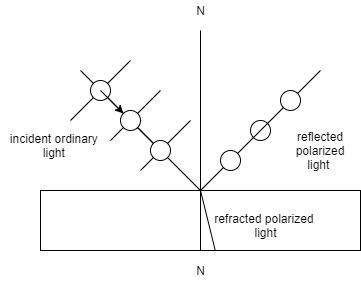
In this figure, it can be seen that an incident unpolarized ray of light breaks down into a refracted ray of light and a reflected ray of light.
Let the refractive index of medium 1 is ${n_1}$ and that of medium 2 is ${n_2}$ . Using Snell’s law,
${n_i}\sin {\theta _i} = {n_r}\sin {\theta _r}.........(1)$ where ${\theta _i}\& {\theta _r}$ are the angle of incidence and angle of refraction respectively.
Brewster’s angle is denoted by ${\theta _B}$ and angle of reflection by ${\theta _r}$ .
We know ${\theta _i} = {\theta _{refl}}$
$\therefore$ $(1)$ becomes ${n_1}\sin {\theta _B} = {n_2}\sin {\theta _r}$
$\Rightarrow \sin {\theta _r} = \dfrac{{{n_1}}}{{{n_2}}}\sin {\theta _B}.............(2)$
Consider the figure,
$\Rightarrow{\theta _{ref}} + {90^0} + {\theta _r} = {180^o}$ (Angle of straight line)
$\Rightarrow {\theta _r} = {90^0} - {\theta _{ref}}............(3)$
$(3)$ can be written as ${\theta _r} = {90^0} - {\theta _B}$............$(4)$
because ${\theta _i} = {\theta _{refl}}$
Using $(2)\& (4)$ ,
$\Rightarrow \sin ({90^0} - {\theta _B}) = \dfrac{{{n_1}}}{{{n_2}}}\sin {\theta _B}$
$\therefore \cos {\theta _B} = \dfrac{{{n_1}}}{{{n_2}}}\sin {\theta _B}$ as $\sin ({90^0} - \theta ) = \cos \theta$
$\therefore \dfrac{{{n_2}}}{{{n_1}}} = \dfrac{{\sin {\theta _B}}}{{\cos {\theta _B}}} = \tan {\theta _B}$ as $\dfrac{{\sin \theta }}{{\cos \theta }} = \tan \theta$
$\therefore {n_{21}} = \tan {\theta _B}$ where ${{{n}}_{21}}$ is refractive index of medium $2$ with respect to medium $1$

Note: Refractive index of a medium with respect to another one depends on both the medium and hence when one medium is replaced by another, the Brewster’s angle also changes.
Using inverse trigonometry, we can directly evaluate the Brewster’s angle as
${\theta _B} = {\tan ^{ - 1}}({n_{21}})$