Question
Question: What is meant by the term “two radians” ?...
What is meant by the term “two radians” ?
Solution
To solve this question we need to have the knowledge of angles. Radian is a unit of measures for angles. It is basically an angle formed at the centre of the circle by an Arc of certain length. Arc is defined as the part of a curve, to be more precise it is part of a circumference of a circle.
Complete step-by-step solution:
The question asks us the definition of “two radian”. Radian is the unit for the measurement of the angle which is formed by the arc of the circle at the centre of the circle. Another definition for radian is the ratio of the arc length to the radius of the circle. Mathematically it will be written as:
⇒Radian =rs , here s is the arc length and r is the radius of the circle.
“Two radian” in terms of arc is when the length of the arc formed is twice the length of the radius, which means the value of s is twice the value of r.
⇒rs
Substituting the value of s with r we get:
⇒r2r
Since both the numerator and the denominator contain the term r, so both cancelled, hence we get:
=2 Radian
The above term of “Two Radian” in diagram form is represented as:
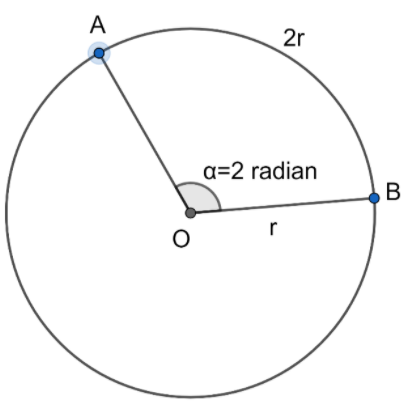
In the above diagram the arcAB⌢ is twice the value of the radius of the circle.
Note: The angle measured in terms of radian could be changed into degree. !!π!! Radian=180∘. So 1 Radian is written as:
⇒1 Radian = π180∘
To find the area and the length of the part of a circle angle is measured in the unit of radian.
