Question

What is meant by the refractive index?

Answer 1

Hint : We will try to understand the term refractive index which is defined as the ratio of the velocity of light in a vacuum to the velocity of light in the given medium. It is also defined as the measure of the bending of light when it passes from one medium to another medium which is also known as an index of refraction.

Complete step by step answer
We will start with the law of refraction which states that the incident ray, refracted ray, and normal all lie in the same plane. Given below is the figure for the example of the refraction of light.

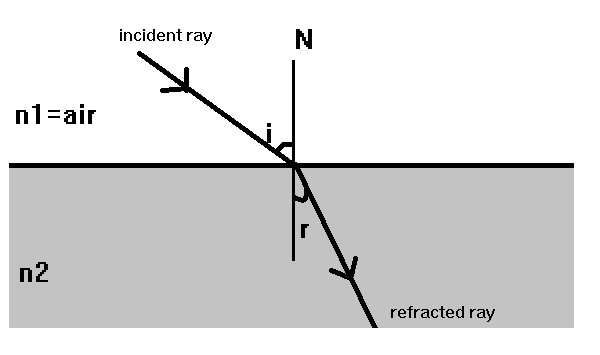
Here $i$ is the angle of incidence which is the angle between the incident ray and normal $N$ to the medium, $r$ is the angle of refraction which is the angle between the refraction ray and normal $N$ to the medium, and ${\eta _1}$ , ${\eta _2}$ can be defined as refractive indices of the given respective medium.
Now the refractive index can be defined as the ratio of the sine of the angle of incidence $i$ to the sine angle of refraction $r$
Hence the refractive index $\eta$ can be given as
$\Rightarrow \eta = \dfrac{{\sin i}}{{\sin r}}$
The Refractive index as discussed can also be defined as the ratio of the velocity of light $c$ in a vacuum and the velocity of the light $v$ in a given medium. Hence
$\Rightarrow \eta = \dfrac{c}{v}$ .

Note
The velocity of the light in a vacuum is always constant which can be given as $c = 2.99 \times {10^8}\dfrac{m}{s}$ . Hence the refractive index of any medium always depends on the velocity of light in that medium. The refractive index of air is ${\eta _{air}} = 1.0003$ while the refractive index of some medium such as water is ${\eta _{water}} = 1.333$ and for crown glass ${\eta _{crownglass}} = 1.517$ and for a diamond it is ${\eta _{diamond}} = 2.417$ .