Question

What is meant by polar form and rectangular form ? How do you find them for complex equations?

Answer 1

In this question, we need to explain what polar form and rectangular form is .Mathematically, There are two basic forms of complex number notation namely polar and rectangular. To answer this kind of problem we need to know the concept of rectangular form and polar form of coordinates. Then we have to explain how the polar and the rectangular form can be found with the help of a simple example for a complex equation.

Complete step by step solution:
Polar form :
The polar form of a complex number is nothing but the way to represent a complex number apart from the rectangular form. The polar form is a form of complex number which is denoted by the length and the angle of its vector . But in the polar form, we used to represent the complex numbers as the combination of modulus and argument. The polar coordinates are $(r,\ \theta)$ .
Now we can find the polar coordinate form of the complex number.

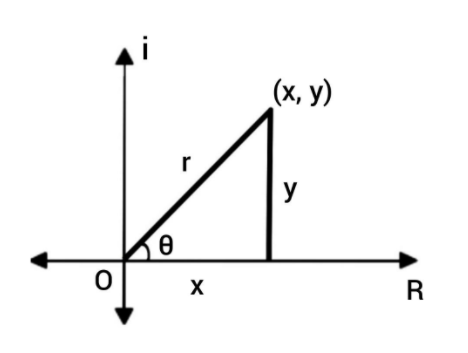
The x axis is the real axis and the y axis is the imaginary axis. We have found the real and complex components in terms of $r$ and $\theta$ where $r$ is the length of the vector and $\theta$ is the angle made with the real axis.
From the Pythagoras theorem,
$\Rightarrow \ r^{2} = x^{2} + y^{2}$
By using the trigonometric ratios, we know that cosine is adjacent to the Hypotenuse.
$\cos\ \theta = \dfrac{x}{r}$
On multiplying both sides by $r$ ,
We get,
$\Rightarrow \ r\ \cos\ \theta = x$
Also sine is opposite to the hypotenuse.
$\sin\ \theta = \dfrac{y}{r}$
On multiplying both sides by $r$,
We get,
$\Rightarrow \ r\ \sin\ \theta = y$
The rectangular form of a complex number is given by $z = x + iy$
On substituting $x$ and $y$,
We get,
$\Rightarrow \ z = r\ \cos\ \theta + \ i(r\ \sin\ \theta)$
By taking $r$ common,
We get,
$\Rightarrow \ z = r(\cos\ \theta + \ i(\sin\ \theta))$
Where $r$ represents the absolute value and $\theta$ represents is the argument of the complex number and $r = \left| z \right| = \sqrt{x^{2} + y^{2}}$ and also $\theta = \tan^{- 1}\left( \dfrac{y}{x} \right)$ for $x > 0$ and for $x < 0$ , $\theta = \tan^{- 1}\left( \dfrac{y}{x} \right) + \pi$
Thus the polar form of the complex number $z = x + iy$ is $r(\cos\ \theta + \ i(\sin\ \theta))$
Rectangular form :
Rectangular form of a complex number is denoted by its respective horizontal and vertical components.
The rectangular coordinate form of a complex number is $z = x + iy$ .
The rectangular coordinates are $(x,\ y)$ .
Now we consider a complex number $( - 1 + i)$
First we can find the polar form of $( - 1 + i)$
The general form of the complex number is $(x + iy)$
By comparing,
We get,
$x = - 1$ and $y = 1$
First we can find $r$,
$\Rightarrow \ r = \sqrt{x^{2} + y^{2}}$
On substituting the values,
We get,
$r = \sqrt{\left( - 1 \right)^{2} + \left( 1 \right)^{2}}$
On simplifying,
We get,
$\Rightarrow \ r = \sqrt{2}$
Also we know that $\cos\ \theta = \dfrac{x}{r}$ and $\sin\ \theta = \dfrac{y}{r}\$
Thus by substituting the values,
We get, $\cos\ \theta = - \dfrac{1}{\sqrt{2}}$ and $\sin\ \theta = \dfrac{1}{\sqrt{2}}$
Now we need to find $\theta$,
We know that $\theta = \tan^{- 1}\left( \dfrac{y}{x} \right)$
On substituting $x$ and $y$ ,
We get,
$\Rightarrow \ \theta = \tan^{- 1}\left( \dfrac{1}{- 1} \right)$
On simplifying,
We get
$\Rightarrow \ \theta = \dfrac{- \pi}{4}$
Thus the polar form of $( - 1 + i)$ is $\sqrt{2}\left( \cos \left( \dfrac{- \pi}{4} \right) + i\ \sin\left( \dfrac{- \pi}{4} \right) \right)$
The polar coordinates are $\left( \sqrt{2},\dfrac{- \pi}{4} \right)$
We need to know that $( - 1 + i)$ is the rectangular form of the complex number. The rectangular coordinates are $( - 1,1)$ .
The polar form of a complex number is nothing but another way to represent a complex number apart from the rectangular form $z = x + iy$ .

Note:
First we should know what a complex number is. Mathematically, complex numbers are represented as $x\ + \ iy$ where $x$ and $y$ are the real numbers and here $i$ is an imaginary number. The set of complex numbers is basically denoted by $C$. Usually, complex numbers consist of two parts namely real parts and imaginary parts . A rectangular equation usually composed of variables like $x$ and $y$ which can be graphed on a regular Cartesian plane whereas a polar equation usually describes a relation between $r$ and $\theta$ , where r represents the distance from pole to a point on a curve, and $\theta$ represents the clockwise angle made by a point on a curve, the pole, and the positive x – axis.