Question

What is ${{\left( \ln x \right)}^{2}}$?

Answer 1

We first find the intercepts of the given function $f\left( x \right)={{\left( \ln x \right)}^{2}}$ which also gives us the roots of the function. Then we use the differentiation to find the extremum points of the function and draw the graph.

Complete step by step solution:
We need to find the zeros, y intercepts of the curve $f\left( x \right)={{\left( \ln x \right)}^{2}}$.
Here the zeroes mean the x intercepts or the roots of the polynomial.
We put the value of $f\left( x \right)=0$ and get ${{\left( \ln x \right)}^{2}}=0$ which gives the roots as $x=1$.
To find the y intercepts we have to put the value of $x=0$ but the logarithmic part of the function ${{\left( \ln x \right)}^{2}}$ is not defined at $x=0$. There are no y intercepts.
Therefore, to find the extremum points we have to find the first and second order derivatives.
Extremum points in a curve have slope value 0.
The slope of the function $f\left( x \right)={{\left( \ln x \right)}^{2}}$ can be found from the derivative of the function ${{f}^{'}}\left( x \right)=\dfrac{d}{dx}\left[ f\left( x \right) \right]$.
We differentiate both sides of the function $f\left( x \right)={{\left( \ln x \right)}^{2}}$ with respect to $x$.
$\begin{aligned} & f\left( x \right)={{\left( \ln x \right)}^{2}} \\\ & \Rightarrow {{f}^{'}}\left( x \right)=\dfrac{d}{dx}\left[ f\left( x \right) \right]=\dfrac{2\ln x}{x} \\\ & \Rightarrow {{f}^{''}}\left( x \right)=\dfrac{d}{dx}\left[ {{f}^{'}}\left( x \right) \right]=\dfrac{2-2\ln x}{{{x}^{2}}} \\\ \end{aligned}$.
To find the $x$ coordinates of the extremum point we take $\dfrac{2\ln x}{x}=0$.
The solution is $2\ln x=0$ which gives $x=1$.
Therefore, from the value of the $x$ coordinates of the extremum points, we find their $y$ coordinates.
The value of the ${{f}^{''}}\left( x \right)$ at $x=1$ is ${{f}^{''}}\left( 1 \right)=\dfrac{2-2\ln x}{{{x}^{2}}}=2>0$. The point at $x=1$ is the minimum value of the function.
Therefore, the extremum point is $\left( 1,0 \right)$.

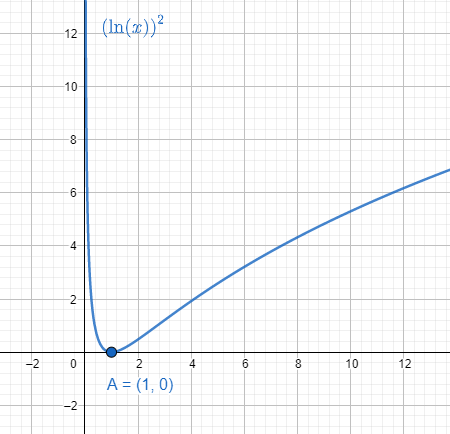
Note: We need to remember that the curve changes its direction on the extremum points only. Other that the function $f\left( x \right)={{\left( \ln x \right)}^{2}}$ is an increasing function in the range of $x\in \left[ 1,\infty \right)$.