Question

What is Doppler Effect? Obtain an expression for the apparent frequency of sound heard when the source is in motion with respect to an observer at rest.

Answer 1

Hint: When a person saying something to another, does so by being in motion, the observer hears a different frequency of the sound wave than the original frequency. This change in the frequency of the sound wave is due to the movement of the source or the observer with respect to each other. The Doppler Effect defines this phenomenon.

Formula Used:
\eqalign{ & Speed,{\text{v}} = \dfrac{{{\text{Distance }}}}{{{\text{Time}}}} \cr & Frequency,v = \dfrac{1}{{{\text{Time Period}}}} \cr}

Complete step-by-step answer:
The apparent change in the frequency of the wave due to motion of the source or the observer with respect to each other is known as Doppler Effect.
Now, suppose an observer is at rest with respect to the medium and the source moves towards the observer with a speed $u$ which is less than the wave speed ${\text{v}}$.

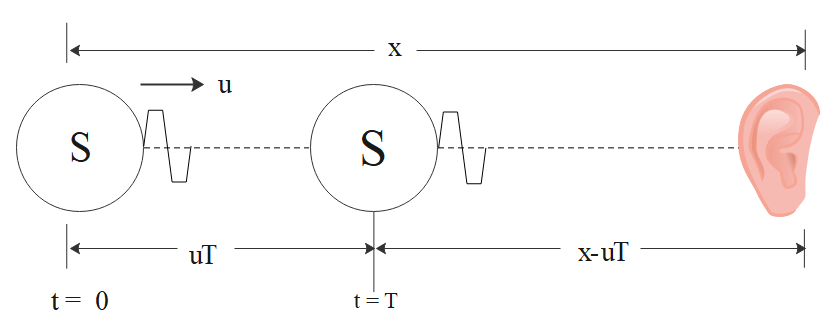
If the frequency of vibration of the source is ${v_ \circ }$, it sends compression pulses at a regular interval of $T = \dfrac{1}{{{v_ \circ }}}$. Suppose the separation between the source and the observer is $x$ when the compression pulse is emitted at $t = 0$. The next compression pulse will be emitted after a time T. The source will travel a distance $uT$ in this time and hence this second compression pulse is emitted from a distance of $x - uT$ from the observer. The first impulse takes time $\dfrac{x}{v}$ to reach the observer while the next one takes $\dfrac{{x - uT}}{v}$.

Thus, the first compression wave reaches the observer at ${t_1} = \dfrac{x}{v}$and the second compression wave reaches at ${t_2} = T + \dfrac{{x - uT}}{v}$. The time interval between the two consecutive compression pulses detected by the observer is given by:

& {T'} = {t_2} - {t_1} \\\ & {T'} = T + \dfrac{{x - uT}}{v} - \dfrac{x}{v} \\\ & = \left( {1 - \dfrac{u}{v}} \right)T \\\ & = \dfrac{{v - u}}{v}T \\\ \end{aligned}$$ The apparent frequency of the sound as experienced by the observer is $$\begin{aligned} & {v'} = \dfrac{1}{T'} & {\text{or, }}{v'} = {\dfrac{v}{v - u}}{v_ \circ } \end{aligned}$$ Similarly, if the source recedes from the observer at a speed u, then the apparent frequency will be: ${\text{ }}{v'} = \dfrac{v}{{v + u}}{v_ \circ }$ Note: Doppler Effect has many important applications related to sensing of movement, for example the machine used by doctors to measure the rate of flow of blood in a patients’ body. Additionally, this Doppler Effect can also be observed in light waves other than the sound waves only.