Question
Question: What is current flowing through the \(6V\):- \(\begin{aligned} & a)125V \\\ & b)12.5V \\\ ...
What is current flowing through the 6V:-
a)125Vb)12.5Vc)1.25Vd)2.5V
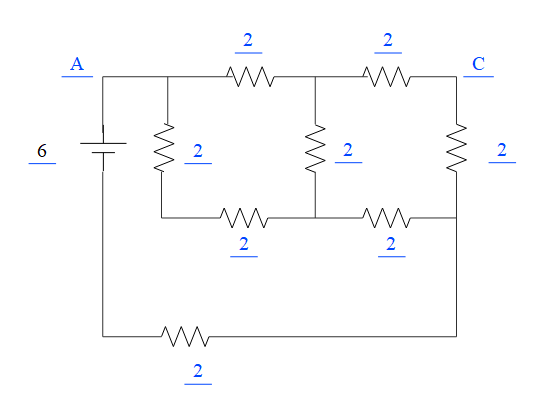
Solution
Check if any of the resistors are connected in series. If so, club them to a single resistor with net resistance. Next, apply Kirchhoff’s voltage law and find the currents through each loop. Finally, we will get the current through each loop including the current through the voltage.
Formula used: ∑iR=0
Req=R1+R2
Complete step by step answer:
Let us find out for any resistors in series, if we see the circuit, there are two combinations of resistors that can be combined in series resistance. Therefore, the net resistance of these two resistors will be equal to.
Req=2+2=4Ω
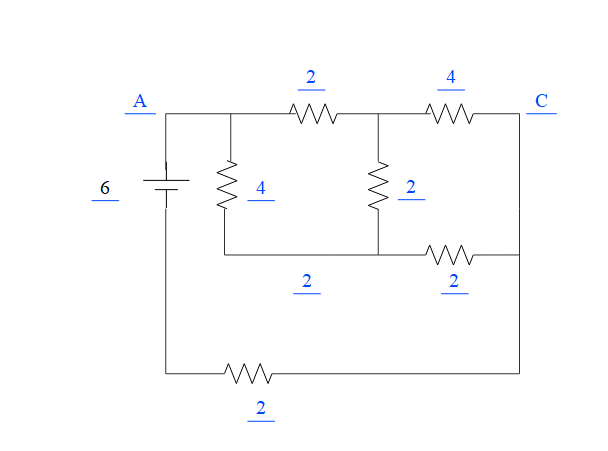
Now, applying Kirchhoff’s law to the above circuits, we get,
For the first loop,
−4i2+2(i1−i2)+2i1=0i1=23i2
Next, let’s find the equivalent resistance inside the circuit, we get
(i1+i2)Req=2i1+4i2Req=514Ω
Now, if we apply ohm's law for the whole circuit, we get,
V=iR6=i(514)i=1.25A
So, the correct answer is “Option C”.
Additional Information: Kirchhoff’s loop rule states that the sum of all electric potential difference around a loop is zero. It is sometimes called Kirchhoff's voltage law or Kirchhoff’s second law. It is called Kirchhoff's voltage law because while calculating, we add the voltage to zero. Kirchhoff's voltage law is an application of the conservation of energy in terms of electric potential difference. The loop rule can also be stated in this way- in a circuit, when charges move through potential difference, its potential difference must be the same when it goes around a complete loop or circuit.
Note: While solving the Kirchhoff’s loop law or the Kirchhoff’s second law, we sometimes get the current passing through the circuit as negative. It means that the current in that loop is travelling in the opposite direction. Thus, it usually happens if we consider the current direction in a wrong way while solving for it.
