Question

What is a transformer? Explain the principle, construction, working and theory of a transformer.

Answer 1

Hint – You can start by defining what a transformer is. Then move on to describe the principle behind the transformer. Then describe the basic setup of a transformer. Then finally write how a transformer works.

An electrical device that can change the A.C. current is known as a transformer.
Principle – A transformer works on the principle of mutual induction. Mutual induction is the phenomenon by which when the amount of magnetic flux linked with a coil changes, an E.M.F. is induced in the neighboring coil.

Construction –
A transformer is made up of a rectangular iron core. Two coils, a primary $({P_{}})$ coil with two sides ${P_1}$ and ${P_2}$, and a secondary $(S)$ coil with two sides ${S_1}$ and ${S_2}$. Both these coils are insulated from the Ferro-magnetic iron core. The source of the alternate current is connected to the primary winding and the output is obtained through the secondary winding which is connected in parallel to a resistance $R$.

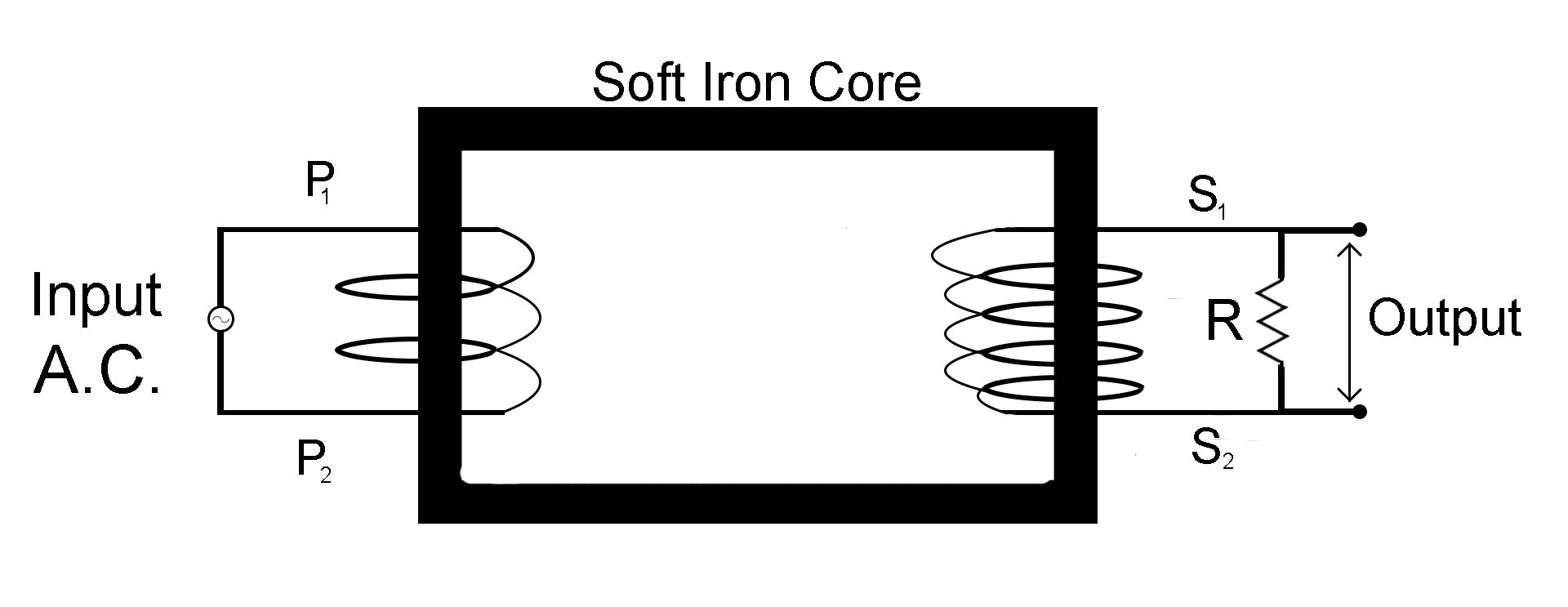
Working -
For an ideal transformer, we consider that resistances of the primary and secondary coils are negligible.
Let the $E.M.F.$ of the alternate current supplied by the A.C source be
${E_P} = {E_0}\sin \omega t$
Let’s assume that the primary winding to be a pure inductance, so here ${I_p}$will lag behind the voltage ${E_{P}}$ by $90^\circ$. Thus the power factor for primary coil becomes,$\cos \phi = \cos 90^\circ = 0$.
Let that the number of turns in primary wire be ${N_P}$ and secondary wire be ${N_S}$
According to faraday law, the induced $E.M.F.$ through one turn of both the coils will be the same.
Let the flux through one turn be $\phi$, the flux through the primary coil be ${\phi _p}$ and the flux through the secondary coil be ${\phi _S}$.
So ${\phi _p} = {N_P}\phi$
${\phi _S} = {N_S}\phi$

We also know by Faraday’s law

$E = \dfrac{{d\phi }}{{dt}}$
So for the primary coil this equation becomes
${E_S} = \dfrac{{d{\phi _S}}}{{dt}}$(Equation 1)
And for the secondary coil this equation becomes
${E_P} = \dfrac{{d{\phi _P}}}{{dt}}$(Equation 2)

Dividing equation 1 by equation 2
$\dfrac{{{E_S}}}{{{E_P}}} = \dfrac{{d{\phi _S}}}{{d{\phi _P}}} = \dfrac{{{N_S}\phi }}{{{N_P}\phi }}$
${E_S} = {E_p}\dfrac{{{N_S}}}{{{N_p}}}$(Equation 3)
We know that
$P = VI$
Here
$P =$Power
$V =$Voltage
$I =$Current
For primary coil this equation becomes
${P_P} = {E_P}{I_P}$(Equation 4)
For secondary coil this equation becomes
${P_S} = {E_S}{I_S}$(Equation 5)
For an ideal transformer no energy is lost, so
${P_p} = {P_S}$
${E_P}{I_P} = {E_S}{I_S}$
${I_S} = {I_p}\dfrac{{{E_p}}}{{{E_s}}}$ $(\because \dfrac{{{E_p}}}{{{E_S}}} = \dfrac{{{N_p}}}{{{N_S}}})$
${I_S} = {I_p}\dfrac{{{N_p}}}{{{N_S}}}$

Note – A transformer that increases the A.C. voltage is known as a step up transformer (${N_S} > {N_p}$) and the transformer that decreases the A.C. voltage is known as a step down transformer (${N_S} < {N_p}$). Additionally an iron core is used because it is a ferromagnetic material which helps in increasing the strength of the magnetic field.