Question

What is a simple pendulum? What type of motion does it have?

Answer 1

A simple pendulum is a mass (say $m$ ) hung by a string of length (say $L$ ). So, the time period of the pendulum is given by the equation $T = 2\pi \sqrt {\dfrac{L}{g}}$ and the equation for the simple harmonic motion of a simple pendulum is $A = {A_0}\cos \left( {\omega t + \phi } \right)$ .

Complete answer:
A simple pendulum consists of a mass $m$ hanging from a string of length $L$ and is fixed at a pivot point. When this pendulum is displaced from its rest position to an initial angle and released, the pendulum will swing to and fro with periodic motion.

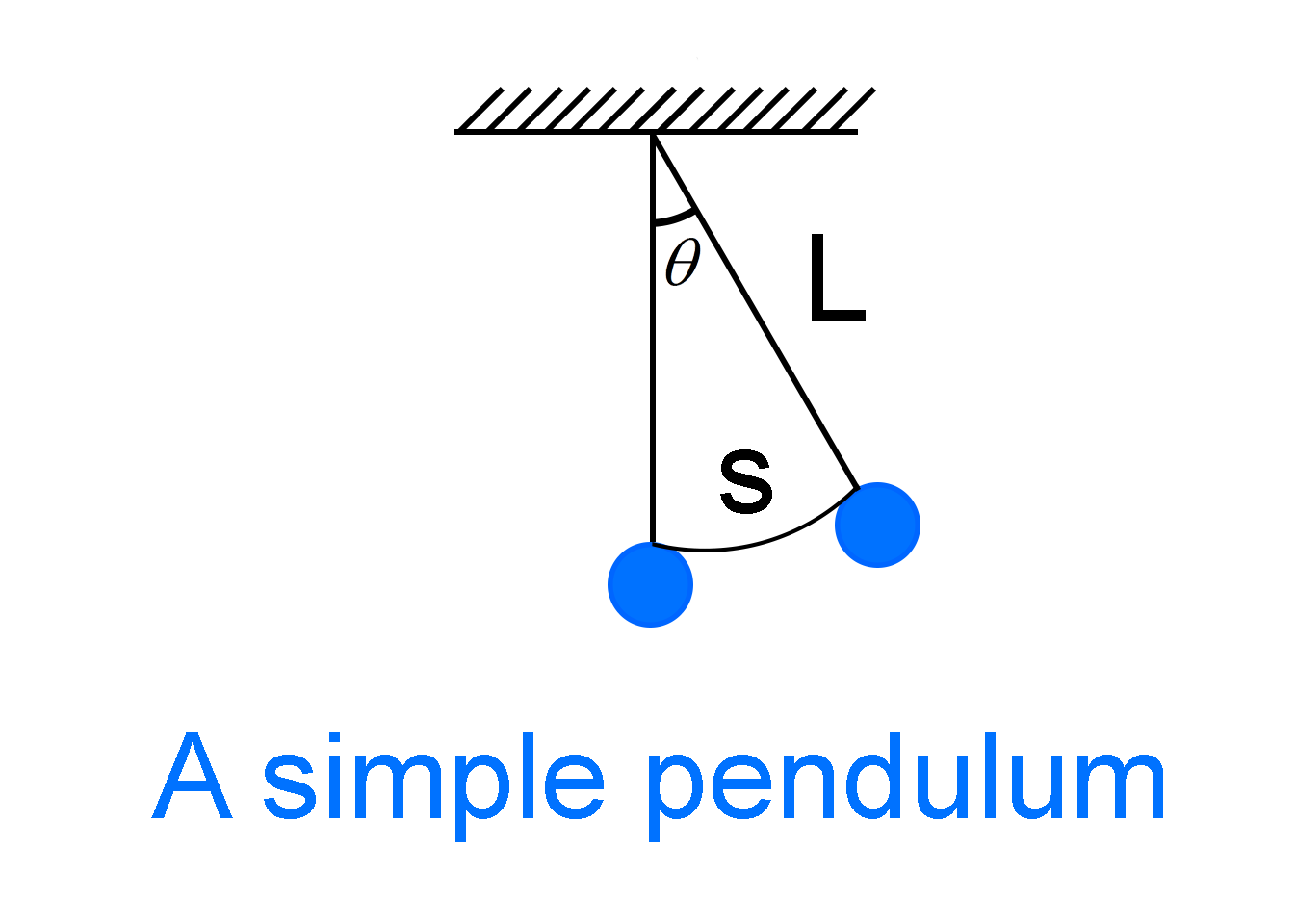
While the equation is not in the rest position a restoring force acts on the simple pendulum which tries to restore the pendulum to its rest position.
The restoring force is given by the following equation
$F = - mg\sin \theta$
The negative sign indicates that the force acts in a direction opposite to the movement of the pendulum.
If the displacement of the pendulum is small, then $\sin \theta = \theta$
$F \approx - mg\theta$
We know that the angle that the arc makes at the pivot point is equal to
$\theta = \dfrac{s}{L}$
$\theta =$ The angle that the pendulum makes at the pivot pointS
$s =$ Displacement of the pendulum
$L =$ Length of the pendulum string
So, $F \approx - mg\dfrac{s}{L}$ (Equation 1)
We also know that the equation for restoring force for rotational motion is
$F = - k\theta$ (Equation 2)
Here, $x =$ Force constant
Comparing equation 1 and 2, we get
$- mg\theta = - kx$
$k = \dfrac{{mg}}{L}$
We know that the equation for the time period of a pendulum is
$T = 2\pi \sqrt {\dfrac{m}{k}}$
Here, $T =$ The time period
$m =$ Mass
$k =$ Force constant
So, for a simple pendulum, this equation becomes
$T = 2\pi \sqrt {\dfrac{m}{{\dfrac{{mg}}{L}}}}$
$T = 2\pi \sqrt {\dfrac{L}{g}}$
The simple pendulum has a simple harmonic motion and the equation for a simple harmonic motion for a simple pendulum is
$A = {A_0}\cos \left( {\omega t + \phi } \right)$
Here, $A =$ The amplitude at time $t$
${A_0} =$ Maximum amplitude
$\omega =$ Angular frequency
$\phi =$ Phase

Note:
The equation for the time period that we obtained, i.e. $T = 2\pi \sqrt {\dfrac{L}{g}}$ gives us a very interesting result. By this equation, we see that the time period of a simple pendulum only depends on the length of the string and the gravity. So, if we measure the time period and length of the string precisely, we can calculate the gravity of a planet.