Question
Question: What is A and B in the hyperbola equation?...
What is A and B in the hyperbola equation?
Solution
We are given a hyperbola and we have to define the terms used in the equation of hyperbola. We know that a hyperbola is a curve with two branches, an open figure, but it is always symmetrical in nature. The equation of a hyperbola is, a2(x−h)2−b2(y−k)2=1, where (h,k) is the centre and ‘a’ is the transverse axis and ‘b’ is the conjugate axis.
Complete step by step answer:
According to the given question, we are asked about the equation of the hyperbola and the terms used in it.
We will begin with the definition of a hyperbola.
A hyperbola is a curve with two branches, and it is an open figure. But in any case, a hyperbola is always symmetrical. If we are to write the expression for a general hyperbola it would be,
a2(x−h)2−b2(y−k)2=1, where (h,k) is the centre and ‘a’ is the transverse axis and ‘b’ is the conjugate axis
And also if the ‘b’ is the transverse axis and ‘a’ the conjugate axis, then the equation of the hyperbola is,
a2(y−h)2−b2(x−k)2=1
Depending upon the transverse axis, the equation of the hyperbola changes.
An example of a hyperbola is as follows,
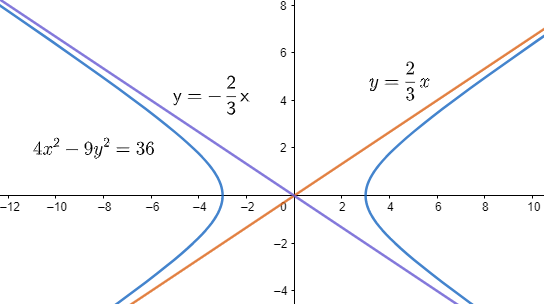
Therefore, ‘a’ is the transverse axis and ‘b’ is the conjugate axis.
Note: While expressing a hyperbola, first check for the transverse axis whether it is in the x – direction or in the y – direction, accordingly use the above given equations of the hyperbola. Similarly, we can also expect questions on concepts of an ellipse or any other conic section. So, we must know all general equations and the terms in each one of them.
