Question

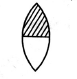
What happens to the image, if a convex lens is made up of two different transparent materials, as shown in the figure?

Answer 1

Hint The convex lens which is made by two different materials has different refractive indices. So they have two different focal lengths. Thus, this type of convex lens forms two different images corresponding to half part of each lens.

Complete step-by-step solution :
Convex lens :
->The convex lens converges the light rays and hence a convex lens is also called a converging lens.
->The image for a far away object is REAL, INVERTED, DIMINISHED and on the opposite side of the lens.
Refractive Index describes the degree to which light rays are bent as they pass from one material to another. When light passes through the interface between two materials of different refractive indices, it is bent.
Refractive index of a lens calculated by two methods :
1)The refractive index calculated by using lensmaker's equation for convex lens is-$\dfrac{1}{f} = \left( {n - 1} \right)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}} + \left( {n - 1} \right)\dfrac{d}{{n{R_1}{R_2}}}} \right)$
Where f is the focal length of the lens,
${R_1}$ is the radius of the first surface,
${R_2}$ is the radius of the second surface,
n is the refractive index of the lens.
To use this equation to find the refractive index, you need to determine f, ${n_1}.\sin {\theta _1} = {n_2}.\sin {\theta _2}$ and ${R_2}$ Using simple trigonometry, you can determine the radius of curvature for each surface. Plug the values of f, R1, and R2 in the equation and solve for n.

2. Another method to find refractive index by measuring the focal length of the lens when it is immersed in liquids of different known refractive index. Three such measurements, even if ${R_1}$and ${R_2}$ are not known are sufficient to give you a set of simultaneous equations that can be solved for n.
   A light wave incident upon a plane surface separating two media of refractive index ${n_1}$and ${n_2}$is refracted upon entering the second medium if the incident wave is oblique to the surface.
   The incident angle (θ1) is related to the refraction angle (θ2) by Snell's law :
   ${n_1}.\sin {\theta _1} = {n_2}.\sin {\theta _2}$

As shown in the above figure, the lens is made up of two different transparent materials.
The above portion of the lens is made up of one transparent material whereas the below portion is made up of the other transparent material. As we know different materials have different refractive indexes as well as different materials have different focal lengths.
The light rays which will fall on the above portion of the lens, will form a different image and the light rays which will fall on the below portion of the lens, will form a different image.
Thus, it is obvious to get two different images from this type of convex lens.

Note:-
A convex lens is also called a converging lens and the concave lens is also called a diverging lens.
The properties of images given by a convex lens depending on the position of the object.
Refractive Index is the speed of light in air divided by the speed of light passing through any material.