Question

What does this mean “For what values of $x$ is $f\left( x \right) > 0$ ?”

Answer 1

A function is a binary relation between two sets in which each element of the first set is associated with precisely one element of the second set. The vertical line test makes determining if a relation is a function on a graph relatively simple. The determination of the fact that a relation is a function, can be done theoretically as well. In this question, we have to find the intervals of $x$ for which the function $f\left( x \right)$ is greater than zero. Hence, we will first assume a function and then find the intervals in which the function is positive.

Complete step by step answer:
The given question states that we need to look for values of x such that the function $f\left( x \right)$ assumes a value greater than zero. Here, $f\left( x \right)$ is a function of $x$. We can clarify the meaning of this statement by taking an example. For example; let $f\left( x \right)$ be a function, where $f\left( x \right) = {x^2} - 9$.

Now, $f\left( x \right)$ has to be greater than zero. So, this means that we need to find the values of x for which the function $f\left( x \right) = {x^2} - 9$ is greater than zero. So, we have,
$f\left( x \right) = {x^2} - 9 > 0$
Factorising the left side of the equation using the algebraic identity ${a^2} - {b^2} = \left( {a - b} \right)\left( {a + b} \right)$ , we get,
$\Rightarrow {x^2} - 9 > 0$
$\Rightarrow \left( {x - 3} \right)\left( {x + 3} \right) > 0$
So, the function $f\left( x \right) = {x^2} - 9$ is positive for $x \in \left( { - \inf , - 3} \right) \cup \left( {3,\inf } \right)$.This can also be understood with the help of graph of the function as shown below.

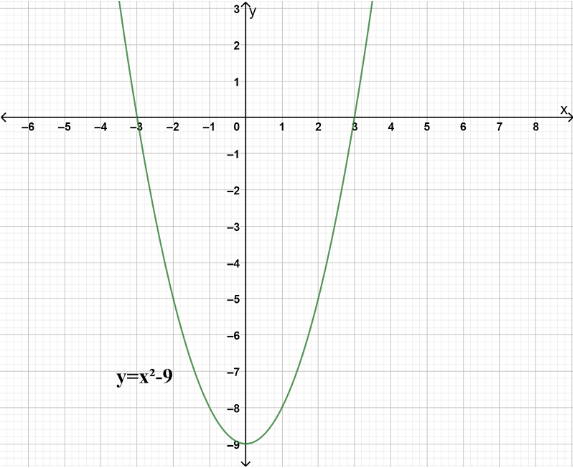
Hence, the values of x for which the function $f\left( x \right) = {x^2} - 9$ is greater than zero are $\left( { - \inf , - 3} \right) \cup \left( {3,\inf } \right)$.

Note: The values of $x$ for which the function attains positive values can be clearly seen in the graph. We arrive at the same answer from both the graphical and theoretical methods. In the graph, the values of $x$ can be seen on the $x$ axis and the values of f(x) can be seen on the $y$ axis. We should know how to solve inequalities in order to find the values of $x$ for which the function is positive.