Question

What does the slope of the velocity-time graph represent?
(A) Distance
(B) Speed
(C) Acceleration
(D) Displacement

Answer 1

Velocity-time graph is helpful in finding the position, distance and the time at which an object is present at a particular position. It is very easy to locate the object by looking at the graph, rather than working out on a formula.

Complete step by step solution:
We know that, slope of a graph is given by,
$\Rightarrow slope = \dfrac{{{\rm{co - ordinates of y - axis}}}}{{{\rm{co - ordinates of x - axis}}}}$
Let us look at an example,

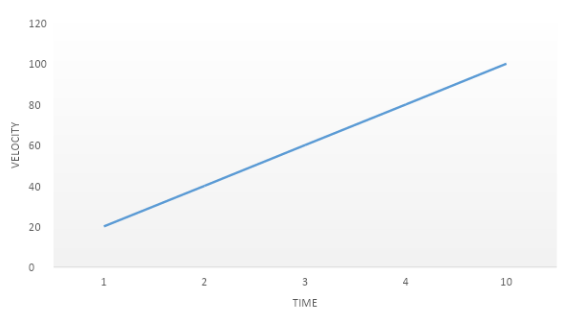
We have plotted a v-t graph for a body. In this graph, let us consider 0-40 m/s velocity (m/s) and the time taken (s) is 2 seconds. Thus, the slope comes as,
$\Rightarrow slope = \dfrac{{40 - 0}}{{2 - 0}}$
$\Rightarrow slope = \dfrac{{40}}{2}m/s/s$
Then the slope is,
$\Rightarrow slope = 20m/s^2$ .
We already know that the acceleration is the quantity that has a SI unit as m/s2.
Hence, the slope of a velocity-time graph represents the acceleration of the body.
Thus, the correct answer is option C.

Note:
-The acceleration or deceleration depends on the slope. The steeper the slope, greater the acceleration. If the line slopes down from left to right direction, that means that the object is slowing down and it denotes deceleration. Deceleration is the negative acceleration. It denotes that the velocity of acceleration is decreasing with time.
-As the slope of a velocity-time graph represents the acceleration of the body, the area under the curve represents the displacement or the distance travelled by the body with the applied velocity and time.
Here, in this graph the area under the graph is also equal to the area of a triangle. If we need to find out the distance travelled by the body in 4 second, the area comes as, $Area{\rm{ of a triangle = }}\dfrac{1}{2} \times base \times height$ .
$\Rightarrow \dfrac{1}{2} \times 4 \times 80 = 160m$
Thus, the distance travelled by the body in 4 seconds is 160 m.