Question

What does the graph of the seventh root of unity look like on a unit circle?

Answer 1

For calculating the position of seven roots of unity on a unit circle, we will us Euler’s form of complex numbers which is given by
$z=\left| z \right|{{e}^{i\theta }}$
Then we will plot those points on the Argand’s plane and join those points together to get the required figure.
For a complex number z,
$\left| {{z}^{n}} \right|={{\left| z \right|}^{n}}$
For ${{n}^{th}}$ roots of unity of a complex number, each root subtends an angle of $\dfrac{2\pi k}{n}$ at the center.

Complete step by step solution:
We have,
${{z}^{7}}=1$
Taking modulus on both sides,
$\left| {{z}^{7}} \right|=1$
As we know that $\left| {{z}^{n}} \right|={{\left| z \right|}^{n}}$
$\begin{aligned} & \Rightarrow {{\left| z \right|}^{7}}=1 \\\ & \Rightarrow \left| z \right|=1 \\\ \end{aligned}$ This means that all the seven roots of unity lie on a circle centered at origin and of radius 1 unit. Now, using Euler’s representation for complex numbers,
$z=\left| z \right|{{e}^{i\theta }}$
$z=1\times {{e}^{\dfrac{i\left( 2\pi k \right)}{7}}}$
For different values of k, we will get different roots of unity.
For k=0
$z=1$ , lying on the real axis.
For k=1,
$z={{e}^{\dfrac{i2\pi }{7}}}$ , lying at an angle of $\dfrac{2\pi }{7}$ from the real axis in an anti-clockwise direction.
For k=2,
$z={{e}^{\dfrac{i4\pi }{7}}}$, lying at an angle of $\dfrac{4\pi }{7}$ from the real axis in an anti-clockwise direction.
.
.
.
For k=6,
$z={{e}^{\dfrac{i12\pi }{7}}}$, lying at an angle of $\dfrac{12\pi }{7}$ from the real axis in an anti-clockwise direction.
For k=7, we will return back to the first root of unity lying on the real axis.
Now, plotting these points on the Argand’s plane, we get

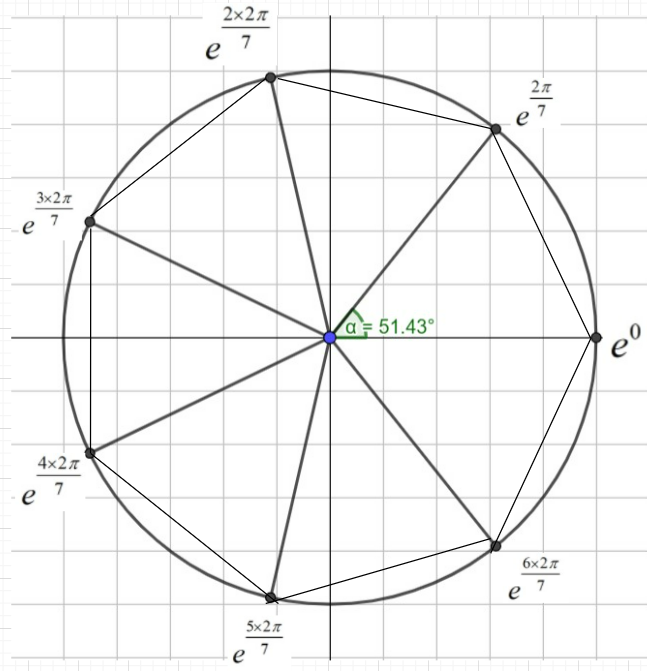
So, on joining the seven roots of unity lying on a circle of unit radius, we get a regular seven-sided polygon.

Note: Each ${{n}^{th}}$ root of unity subtends an equal angle at the center. On joining the roots, we get an n-sided regular polygon. All the n roots of unity always lie on a circle of radius unity. We must remember the formula $z=\left| z \right|{{e}^{i\theta }}$ and not make any mistakes while writing it. If we miss out the terms or add a negative sign, then we will not be able to reach the required results.