Question

What do you understand by wave motion? Clearly explain. Establish the expression and the one dimensional differential equation for a progressive wave.

Answer 1

When continuous particles oscillate about their mean positions at different phases a wave motion is produced. One of the properties of a wave is that it replicates itself after an equal interval of length. Another property of wave motion is that it is a method of transfer of energy.

Complete answer:
We all know what a wave motion is. When continuous particles oscillate about their mean positions at different phases a wave motion is produced. One of the properties of a wave is that it replicates itself after an equal interval of length.
Another property of wave motion is that it is a method of transfer of energy.
There are two types of waves. One is a longitudinal wave and the other is a transverse wave.
In longitudinal waves, the oscillations of the particles are parallel to the propagation of the wave.
In transverse waves, the oscillations of the particles are perpendicular to the propagation of the wave.
Let us establish the wave equation for a transverse wave moving.
Think about a wave motion in a string. The length of the string is x-axis and the oscillations of the particles are along the y-axis.
Let at time t, the displacement of the particle at origin be zero and the displacement of a particle at position x be y.

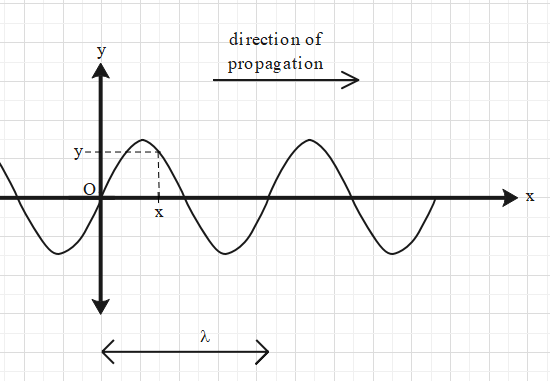
Then from the concept of simple harmonic motion, we get that $y=A\sin \left( \omega t-\phi \right)$ …. (i),
where A is the amplitude of the particles, $\omega$ is the angular frequency of the oscillations and (-$\phi$) is the phase difference between this particle and the particle at the origin.
Now let us use the relation $\dfrac{\phi }{2\pi }=\dfrac{x}{\lambda }$, where $\lambda$ is the wavelength.
$\Rightarrow \phi =\dfrac{2\pi x}{\lambda }$
Substitute the value in equation (i).
$\Rightarrow y=A\sin \left( \omega t-\dfrac{2\pi x}{\lambda } \right)$
Let $\dfrac{2\pi }{\lambda }=k$, where k is a constant called wave number.
$\Rightarrow y=A\sin \left( \omega t-kx \right)$ ….. (ii).
This expression is for the displacement of a particle at a position x, at time t.
Now, differentiate equation (ii) w.r.t time.
$\Rightarrow \dfrac{dy}{dt}=\dfrac{d}{dt}\left( A\sin \left( \omega t-kx \right) \right)$
$\Rightarrow \dfrac{dy}{dt}=A\omega \cos \left( \omega t-kx \right)$ …. (iii).
Again differentiate equation (iii) w.r.t time
$\Rightarrow \dfrac{{{d}^{2}}y}{d{{t}^{2}}}=\dfrac{d}{dt}\left( A\omega \cos \left( \omega t-kx \right) \right)$
$\Rightarrow \dfrac{{{d}^{2}}y}{d{{t}^{2}}}=-A{{\omega }^{2}}\sin \left( \omega t-kx \right)$ …. (iv).
Now, differentiate equation (ii) w.r.t displacement of the particles (x).
$\Rightarrow \dfrac{dy}{dx}=\dfrac{d}{dx}\left( A\sin \left( \omega t-kx \right) \right)$
$\Rightarrow \dfrac{dy}{dx}=-Ak\cos \left( \omega t-kx \right)$
Differentiate again w.r.t x
$\Rightarrow \dfrac{{{d}^{2}}y}{d{{x}^{2}}}=\dfrac{{{d}^{2}}}{d{{x}^{2}}}\left( -Ak\cos \left( \omega t-kx \right) \right)$
$\Rightarrow \dfrac{{{d}^{2}}y}{d{{x}^{2}}}=-A{{k}^{2}}\sin \left( \omega t-kx \right)$ …. (v).
Divide equation (iv) by equation (v).
$\Rightarrow \dfrac{\dfrac{{{d}^{2}}y}{d{{t}^{2}}}}{\dfrac{{{d}^{2}}y}{d{{x}^{2}}}}=\dfrac{-A{{\omega }^{2}}\sin \left( \omega t-kx \right)}{-A{{k}^{2}}\sin \left( \omega t-kx \right)}$
$\Rightarrow \dfrac{{{d}^{2}}y}{d{{t}^{2}}}=\left( \dfrac{{{\omega }^{2}}}{{{k}^{2}}} \right)\dfrac{{{d}^{2}}y}{d{{x}^{2}}}$.
This equation is called the one dimensional differential equation of waves.

Note:
Note that the expression that we found for the displacement of a particle at position x at a given time t is applicable for a particular direction of propagation of the wave (say positive direction). If the wave propagates into the opposite direction (i.e. in negative direction), then the expression for y changes to $y=A\sin \left( \omega t+kx \right)$.