Question

What do you understand by ‘Sharpness of resonance’ for a series LCR resonant circuit? How is it related to the quality factor ‘Q’ of the circuit? Using the graphs given in the diagram, explain the factors which affect it. For which graph is the resistance (R) minimum? KR 0 = 0, 0

$\omega ={{\omega }_{r}}$ $\omega$

Answer 1

Hint : In this question, we find’ what is ‘sharpness of resonance’ for a $LCR$ resonant circuit and it’s related with the quality factor ‘$Q$’ and which factors affect it using the given graph. Here we divided questions into three-part a, b and c.

Complete step by step answer:
(A) We know that in $LCR$circuit, the impedance is given by:
$Z=\sqrt{{{R}^{2}}+{{({{X}_{L}}-{{X}_{C}})}^{2}}}$
Here,
$R$= Resistance of Circuit
${{X}_{L}}$= Inductive Resistance of Circuit
${{X}_{C}}$= Capacitive Resistance of Circuit
At Resonance in $LCR$ Circuit,
${{X}_{L}}={{X}_{C}}$
We can write ${{X}_{L}}$and ${{X}_{C}}$ as,
$\omega L=\dfrac{1}{\omega C}$
On further solving we can write the equation as,
${{\omega }^{2}}=\dfrac{1}{LC}$
We take square root on both sides of the equation,
$\omega =\dfrac{1}{\sqrt{LC}}$
This equation is known as the resonance frequency.
Further, impedance is minimum at resonance.
${{Z}_{\min }}=R$
This means that the current becomes maximum,
${{I}_{\max }}=\dfrac{{{V}_{rms}}}{R}$.
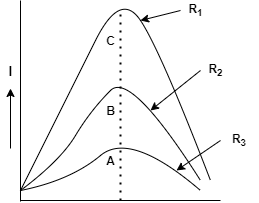
B) The figure shows the variation of current amplitude ${{i}_{m}}$ with frequency $\omega$in $LCR$ circuit for two values of resistance ${{R}_{1}}$ and${{R}_{2}}$. This figure shows that ${{R}_{1}}$ is greater than${{R}_{2}}$.
C) Quality factor or $Q$-factor of a resonant $LCR$ circuit is defined as the ratio of the voltage drop across the capacitor or inductor to that of the applied voltage. It is given by:
$Q=\dfrac{1}{R}\sqrt{\dfrac{L}{C}}$
The $Q$-factor determines the sharpness of the resonance curve. If the resonance is less sharp, not only the maximum current is less, the circuit is closer to resonance for larger values of $\Delta \omega$and frequencies and tuning of the circuit will not be good. So, the less sharp the resonance, the less the selectivity of the circuit while higher the$Q$, sharper the resonance curve and lesser will be the loss of energy in the circuit.

Note: To understand this question we have to study $LCR$circuit, the sharpness of resonance, and the quality factor of the resonant $LCR$ circuit. In this, we find out that impedance is minimum at resonance and in the given figure ${{R}_{1}}$is greater than${{R}_{2}}$. And the $Q$-factor determines the sharpness of the resonance curve. It can be easily solved if you know LCR circuits and their properties.