Question

What do you mean by rectangular components of a vector? Explain how a vector can be resolved into two rectangular components in a plane.

Answer 1

There are majorly two types of quantities, scalar and vector quantities. All the quantities are divided into these two categories. Scalar quantities are those quantities, which have only magnitude eg – mass, speed, pressure, etc. Vector quantities are those which have both magnitude and directions eg – weight, velocity and thrust. The special fact about vectors is that we can resolve it into components.

Complete step by step answer:
Rectangular components means the components or parts of a vector in any two mutually perpendicular axes. This could be understood by an example as illustrated below.

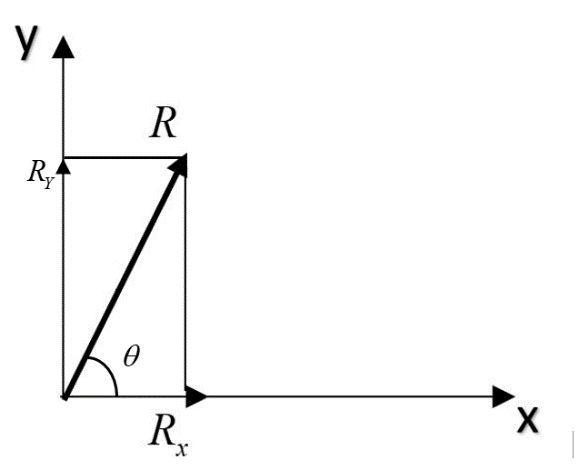
Let a vector quantity ‘R’ inclined at an angle $\theta$ from the x-axis. By convention, we can split the vector ‘R’ in two rectangular components. As shown in the figure, the vector ‘R’ is split into two components;
$R_x$along x-axis and $R_y$ along y-axis. This is an extremely important and useful property of vectors. Using it, we can solve complex problems very easily. Also, we can write the values of these components as;
$R_x = Rcos\theta$
$R_y=Rsin\theta$

Additional Information: For any two general vectors, we have the magnitude of their resultant $R = \sqrt{A^2+B^2+2ABcos\theta}$. Since we have split the given vector ‘R’ into two independent vectors, we can see that doing this won't change the magnitude of the original vector.
Here A = $R_x = Rcos\theta$ and B = $R_y=Rsin\theta$
Hence, putting in the formula:
$R = \sqrt{A^2+B^2+2ABcos\theta}$
$\Rightarrow R = \sqrt{(Rcos\theta)^2+(Rsin\theta)^2+2(Rcos\theta)(Rsin\theta)cos90^{\circ}}$
As $cos\ 90^{\circ} = 0$
$R = \sqrt{R^2[(cos\theta)^2+(sin\theta)^2]+0}$
Also, $sin^2\theta+cos^2\theta = 1$
So, $R = \sqrt{R^2} = R$

Hence proved.

Note: One must not confuse that we can take the vector components only along axes that are mutually perpendicular. One can also find the component of a vector about any axis which inclination with the vector is given, provided the magnitude of the vector must not change.