Solveeit Logo
Login

Question

Question: What are the vertex, axis of symmetry, maximum or minimum value, domain and range of the function \(...

What are the vertex, axis of symmetry, maximum or minimum value, domain and range of the function y=−x2−4x+3y=-{{x}^{2}}-4x+3?

Explanation

Solution

To solve the given question we will use the standard formula of vertex form of parabola y=a(x−h)2+ky=a{{\left( x-h \right)}^{2}}+k , where (h,k)\left( h,k \right) are the coordinates of vertex and (x,y)\left( x,y \right) are the coordinates of point from which parabola passes through and a is the distance of origin from the focus. Then we will find the domain and range of the given function.

Complete step-by-step solution:
We have been given a function y=−x2−4x+3y=-{{x}^{2}}-4x+3.
We have to find the vertex, axis of symmetry, maximum or minimum value, domain and range of the given function.
The given function is quadratic in nature of the form ax2+bx+ca{{x}^{2}}+bx+c. When we compare the given equation with the general equation we will get the values
⇒a=−1,b=−4,c=3\Rightarrow a=-1,b=-4,c=3
Now, we know that the general form of equation of parabola is given as y=a(x−h)2+ky=a{{\left( x-h \right)}^{2}}+k , where (h,k)\left( h,k \right) are the coordinates of vertex and (x,y)\left( x,y \right) are the coordinates of point from which parabola passes through and a is the distance of origin from the focus.
Now, the vertex of parabola will be
⇒h=−b2a and k=y(h)\Rightarrow h=-\dfrac{b}{2a}\text{ and }k=y\left( h \right)
Now, substituting the values we will get
⇒h=−−42×(−1) ⇒h=−−4−2 ⇒h=−2 \begin{aligned} & \Rightarrow h=-\dfrac{-4}{2\times (-1)} \\\ & \Rightarrow h=-\dfrac{-4}{-2} \\\ & \Rightarrow h=-2 \\\ \end{aligned}
Now,
⇒k=y(h) ⇒k=−(−2)2−4(−2)+3 ⇒k=−4+8+3 ⇒k=7 \begin{aligned} & \Rightarrow k=y\left( h \right) \\\ & \Rightarrow k=-{{\left( -2 \right)}^{2}}-4\left( -2 \right)+3 \\\ & \Rightarrow k=-4+8+3 \\\ & \Rightarrow k=7 \\\ \end{aligned}
Now, let us plot a graph for the given equation then we will get

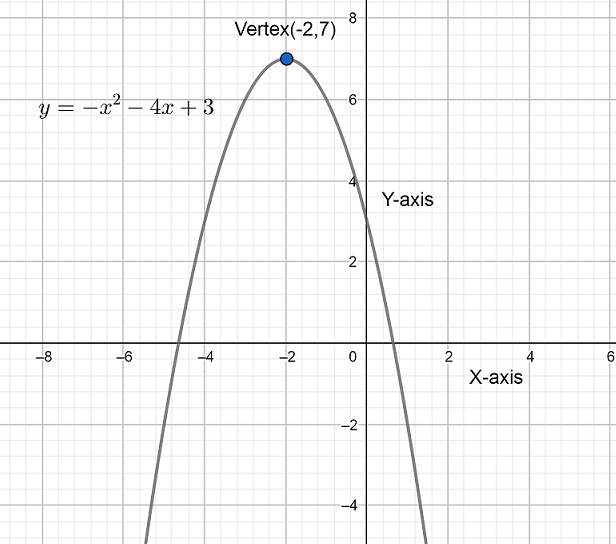
When we observe the above graph we will find that the vertex of parabola is (−2,7)\left( -2,7 \right).
The axis of symmetry is x=−2x=-2.
The maximum value is 7.
The domain of the given function is all real values. So the domain of the function is (−∞,∞)\left( -\infty ,\infty \right) and the range of the function is (−∞,7]\left( -\infty ,7 \right].
Hence we get the required values.

Note: If the value of coefficient of x2{{x}^{2}} is negative then we have to calculate the maximum value. Also if the coefficient of x2{{x}^{2}} is negative then the parabola opens downwards. The coordinate of x is the axis of symmetry.