Question

What are the six trigonometric function values of 540?

Answer 1

Hint : To find the six trig function values of 540, we need to draw the unit circle first. The angle is given in degree so convert it into radian. Now, $540^\circ = 3\pi$ so $\sin 3\pi$ and $\cos 3\pi$ will lie on the X' axis. The values of sine and cosine on X’ axis are given by point $\left( {\cos \theta ,\sin \theta } \right) = \left( { - 1,0} \right)$ . Now, using these two values we can find the remaining 4 trig function values easily.

Complete step by step solution:
In this question, we have to find the six trigonometric function values of 540.
The six trigonometric functions are sin, cos, tan, cosec, sec and cot.
Now, the angle is given in degrees in our question. We have to convert it in radian first of all.
So, to convert degree into radian, we multiply degree with $\dfrac{\pi }{{180}}$ .
Therefore, $540^\circ = 540 \times \dfrac{\pi }{{180}} = 3\pi$ .Now, let us draw a unit circle to find these trig function values.

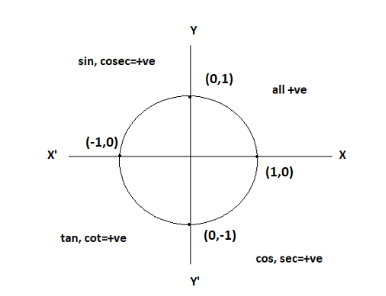
Now, we need to find $\sin 3\pi ,\cos 3\pi ,\tan 3\pi ,\cos ec3\pi ,\sec 3\pi ,\cot 3\pi$ .

1. $\sin 3\pi$
   All the points on the unit circle are represented by $\left( {\cos \theta ,\sin \theta } \right)$
   $3\pi$ lies on the X' axis and the coordinates at X’ axis are $\left( { - 1,0} \right)$ .
   Hence, the value of all $\sin \theta$ on X’ axis will be equal to 0.
   Hence, $\sin \pi = \sin 3\pi = \sin 5\pi = 0$ .
   Therefore, $\sin 3\pi = 0$ .

2. $\cos 3\pi$
   $3\pi$ lies on the X' axis and the coordinates at X’ axis are $\left( { - 1,0} \right)$ .
   Hence, the value of all $\cos \theta$ on X’ axis will be equal to $- 1$ .
   Hence, $\cos \pi = \cos 3\pi = \cos 5\pi = - 1$ .
   Therefore, $\cos 3\pi = - 1$ .

3. $\tan 3\pi$
   We know that $\tan \theta = \dfrac{{\sin \theta }}{{\cos \theta }}$ , and we have the values of $\sin 3\pi$ and $\cos 3\pi$ .
   Therefore, $\tan 3\pi = \dfrac{{\sin 3\pi }}{{\cos 3\pi }}$
   $\Rightarrow \tan 3\pi = \dfrac{0}{{ - 1}} \\\ \Rightarrow \tan 3\pi = 0 \;$

4. $\cos ec3\pi$
   We know that cosec is the inverse of sine. So, we can write $\cos ec\theta$ as $\dfrac{1}{{\sin \theta }}$ .
   $\Rightarrow \cos ec3\pi = \dfrac{1}{{\sin 3\pi }}$
   And $\sin 3\pi = 0$
   $\Rightarrow \cos ec3\pi = \dfrac{1}{0}$
   $\Rightarrow \cos ec3\pi =$ not defined.

5. $\sec 3\pi$
   We know that sec is the inverse of cos. So, we can write $\sec \theta$ as $\dfrac{1}{{\cos \theta }}$ .
   $\Rightarrow \sec 3\pi = \dfrac{1}{{\cos 3\pi }}$
   And $\cos 3\pi = - 1$
   $\Rightarrow \sec 3\pi = \dfrac{1}{{ - 1}} \\\ \Rightarrow \sec 3\pi = - 1 \;$

6. $\cot 3\pi$
   We know that cot is the inverse of tan. So, we can write $\cot \theta$ as $\dfrac{1}{{\tan \theta }}$ .
   $\Rightarrow \cot 3\pi \dfrac{1}{{\tan 3\pi }}$
   And $\tan 3\pi = 0$ .
   $\Rightarrow \cot 3\pi = \dfrac{1}{0}$
   $\Rightarrow \cot 3\pi =$ not defined
   Hence, we have found all the six trig function values of 540.
   $\sin 540^\circ = \sin 3\pi = 0 \\\ \cos 540^\circ = \cos 3\pi = - 1 \\\ \tan 540^\circ = \tan 3\pi = 0 \\\ \cos ec540^\circ = \cos ec3\pi = notdefined \\\ \sec 540^\circ = \sec 3\pi = - 1 \\\ \cot 540^\circ = \cot 3\pi = notdefined \;$

Note : In first quadrant $\left( {0 \leqslant \theta \leqslant \dfrac{\pi }{2}} \right)$ , all the values of trig functions are positive.
In second quadrant $\left( {\dfrac{\pi }{2} \leqslant \theta \leqslant \pi } \right)$ , the values of only sine and cosecant are positive
In third quadrant $\left( {\pi \leqslant \theta \leqslant \dfrac{{3\pi }}{2}} \right)$ , the values of only tangent and cotangent are positive.
In fourth quadrant $\left( {\dfrac{{3\pi }}{2} \leqslant \theta \leqslant 2\pi } \right)$ , the values of only cosine and secant are positive.