Question

What are the local maxima or minima of ${x^3} - 3{x^2} + 1$?

Answer 1

To find the maxima or minima we will first find the derivative of this curve and equate it to zero. This is because at maximum point or minimum point the slope of the tangent is zero and since the derivative gives the slope so, we are equating the derivative to zero. From here we will get two points. Now to know which is the maxima and which is the minima we will use the second derivative rule. We will find the second derivative and put these points in that. If we get a positive number then the point is minimum and if we get a negative number then the point is the maximum point.

Complete step by step answer:
Let, $y = {x^3} - 3{x^2} + 1$
Differentiating both sides we get;
$\Rightarrow \dfrac{{dy}}{{dx}} = \dfrac{{d\left( {{x^3} - 3{x^2} + 1} \right)}}{{dx}}$
Writing separately, we get;
$\Rightarrow \dfrac{{dy}}{{dx}} = \dfrac{{d{x^3}}}{{dx}} - \dfrac{{d3{x^2}}}{{dx}} + \dfrac{{d\left( 1 \right)}}{{dx}}$

On differentiating we have;
$\Rightarrow \dfrac{{dy}}{{dx}} = 3{x^2} - 6x$
Now we will equate it to zero. So, we have;
$\Rightarrow \dfrac{{dy}}{{dx}} = 3{x^2} - 6x = 0$
$\Rightarrow 3{x^2} - 6x = 0$
Now, taking common we have;
$\Rightarrow 3x\left( {x - 2} \right) = 0$
On solving by equating each term to zero, we get;
$\Rightarrow x = 0,2$

Now we have the points of maxima and minima but we do not know which is the maxima and which is the minimum point. For this we will again differentiate the equation. So, we have;
$\Rightarrow \dfrac{d}{{dx}}\left( {\dfrac{{dy}}{{dx}}} \right) = \dfrac{{d\left( {3{x^2} - 6x} \right)}}{{dx}}$
On differentiating we get;
$\Rightarrow \dfrac{{{d^2}y}}{{d{x^2}}} = 6x - 6$
Putting $x = 0$, we get;
$\Rightarrow \dfrac{{{d^2}y}}{{d{x^2}}} = 6 \times 0 - 6$
$\Rightarrow \dfrac{{{d^2}y}}{{d{x^2}}} = - 6$
So, this is a negative number. Hence, $x = 0$ is the point of maxima.

Putting $x = 2$ we get;
$\Rightarrow \dfrac{{{d^2}y}}{{d{x^2}}} = 6 \times 2 - 6$
Solving we have;
$\Rightarrow \dfrac{{{d^2}y}}{{d{x^2}}} = 6$
This is a positive number. So, $x = 2$ is a point of minima.
For $x = 0$, we have;
$y = {0^3} - 3{\left( 0 \right)^2} + 1$
$\Rightarrow y = 1$
Hence, $\left( {0,1} \right)$ is the point of maxima.
For $x = 2$, we have;
$\Rightarrow y = {2^3} - 3{\left( 2 \right)^2} + 1$
$\therefore y = - 3$
Hence, $\left( {2, - 3} \right)$ is the minimum point.
The graph is shown below:

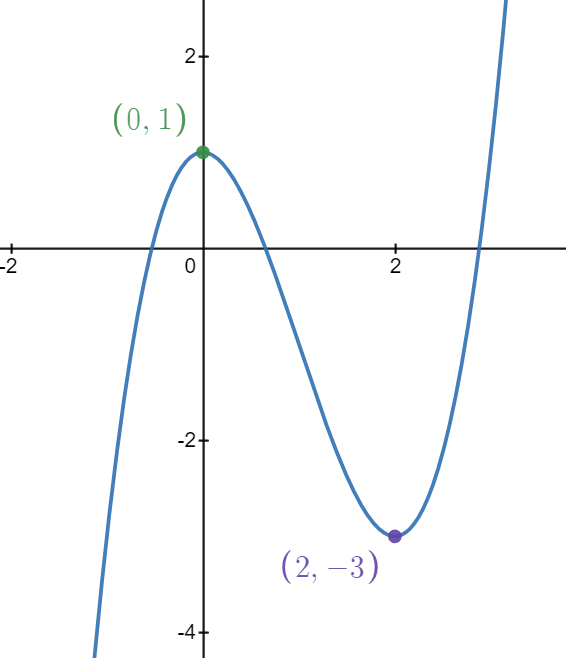
Note: When we see the graph, we get to know that at the minimum point the slope is zero but if we increase the value of $x$, then the value of the function tends to increase and hence the slope is positive. In case of maxima, the slope mat maxima is zero, but when we further increase the value of, then the value of function decreases and hence the slope is negative.