Question

What are the different types of functions?

Answer 1

Here, the given question is about the different types of functions. To solve this theory question, we need to know about the basic definition of function, and types of functions with examples and with relevant diagrams.

Complete step-by-step solution:
The function is defined as the function as a special relation, the function maps each element of set A to exactly one element of set B. Both set A and set B should be non-empty. A function defines a specific output for the specific input.
As a result, $f:A\to B$ is a function in which $a\in A$ there is a unique element $b\in B$ such that $\left( a,b \right)\in f$.
Types of Functions-
One to One Function
Many to One Function
Onto Function
One-One and Onto Function
Identity Function
Constant Function
Polynomial Function
Quadratic Function
Modulus Function
Signum Function
Greatest Integer Function

1. One to One Function: A function $f:A\to B$ is One to One if for each element of A there should be a distinct element of B. It is also known as Injective.
Consider if ${{a}_{1}}\in A$ and ${{a}_{2}}\in B$, f is defined as $f:A\to B$ such that $f\left( {{a}_{1}} \right)={{a}_{2}}$.

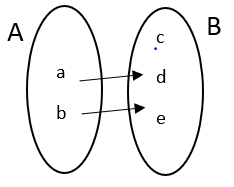
2. Many to One function: A function $f:A\to B$ is many to one if two or more elements of A has same image in B

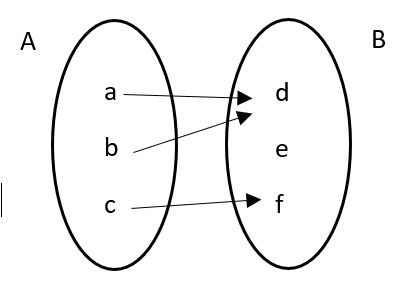
3.Onto function: a function $f:A\to B$ if every element of B is related to at least one element of A. It is also called surjective function.

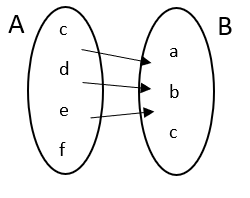
4. One-one and onto function: A function $f:A\to B$ is one-one and onto if it satisfies both the condition for one-one and onto. It is also known as bijective function.

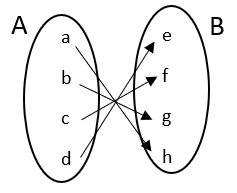
5. Invertible functions: For a function to be invertible it needs to be both one-one and onto function.

6. Composite functions: $f:A\to B$ and $g:B\to C$ can be composed to form a function which maps from A to C. A composite function is denoted by $\left( gof \right)\left( x \right):g\left( f\left( x \right) \right)$.

Note: There are other functions, which are used in mathematical sets topic. Taking the subsets and set improperly, the students do make mistakes in the functions while taking the subsets and set improperly.