Question

What are the conic sections used for?

Answer 1

As we know that there are so many shapes in conic sections that are useful in our practice life for new creation or doing research based on the shapes of conic sections. In Mathematics we use it to derive the shapes of the conic section by its equations. It might be a circle, ellipse, hyperbola or parabola according to the shape of the conic section. Here are the equations for the different conic sections that are below as:

Shape	Equation
Circle	${{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{r}^{2}}$
Ellipse	$\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}+\dfrac{{{\left( y-k \right)}^{2}}}{{{b}^{2}}}=1$
Hyperbola	$\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}-\dfrac{{{\left( y-k \right)}^{2}}}{{{b}^{2}}}=1$
Parabola	${{\left( x-h \right)}^{2}}=4p\left( y-k \right)$

Complete step by step solution:
First of all we'll know about conic sections and its various types. In the conic sections, we will understand about the shapes or curves of conic sections.
“A conic section is obtained from the intersections of plane surfaces and it generates a double napped right circular cone.”
There are various shapes are found when the plane cuts the napped cone and these shapes are:
Circle:

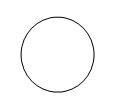
Ellipse:

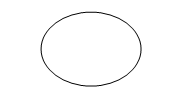
Parabola:

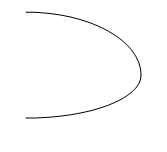
Hyperbola:

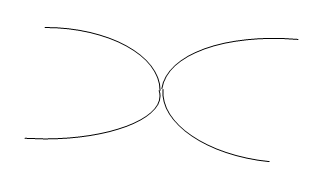
Now, we will try to understand the use of conic sections. There are some examples related to the conic section:
Bangles are in the shape of a circle.
The path of earth is ellipsoid.
Car headlights are an example of parabola.
If we will observe some things carefully in our daily life, we will find that some of them are in the shape of conic sections. It gives varieties of design and solidness to the structure. It helps to create many more things like a designed circular roof or a parabolic shape of roof.
Since, we have equations for every curve of conic section that helps to calculate it according to the dimension what size of the structure would be. Here are the equations of different conic sections as:

Shape	Equation
Circle	${{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{r}^{2}}$
Ellipse	$\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}+\dfrac{{{\left( y-k \right)}^{2}}}{{{b}^{2}}}=1$
Hyperbola	$\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}-\dfrac{{{\left( y-k \right)}^{2}}}{{{b}^{2}}}=1$
Parabola	${{\left( x-h \right)}^{2}}=4p\left( y-k \right)$

Note: We will have to keep some points in minds regarding the shapes of conic sections that are noted below as:
The expression of all conic equation will be in the form of:
$\Rightarrow a{{x}^{2}}+b{{y}^{2}}+cxy+dx+ey+f=0$
Where, $a,b,c,d,e$ and $f$ are constants:
If ${{c}^{2}}-4ab<0$ ,it will be either a circle or an ellipse.
If ${{c}^{2}}-4ab=0$ , it will be a parabola.
If ${{c}^{2}}-4ab>0$, it will be a hyperbola.