Question

What are the asymptotes of $y=\dfrac{1}{{{x}^{2}}}$?

Answer 1

Now considering the given function. First, we will start by defining the asymptote and then check where the function is not defined. We know that function will not be defined when the denominator is 0 and know about the types of asymptotes required for a given question and finally, we draw a graph.

Complete step by step solution:
Asymptotes are defined as the lines which indicates a value towards which the function seems to be approaching but never reaches.
There are three types of asymptotes; they are horizontal, vertical and unique asymptotes.
Let us assume the function $\dfrac{1}{n}$. Now we know that $n\to \infty$ the function $\dfrac{1}{n}\to 0$. Here we can say that the function approaches 0 but never reaches 0 as $\dfrac{1}{n}=0$ is not possible for any natural number n.
Let us solve the question
Vertical asymptotes for rational numbers are found by setting when the denominator is 0. This will also help us to find the domain. The domain cannot contain the number. For this function ${{x}^{2}}\ne 0$
So $x=0$ is the equation of the vertical asymptote, and 0 must be left out of the domain: $\left( -\infty ,0 \right)U\left( 0,\infty \right)$ in interval representation.
Horizontal asymptotes are found by replacing large positive and negative values into the function.$f\left( 1000 \right)$ or $f\left( 1000000 \right)$ can help to determine where the function "ends" are heading. In this case, $\dfrac{1}{{{\left( 1000 \right)}^{2}}}$ or $\dfrac{1}{{{\left( 1000000 \right)}^{2}}}$ will get close to 0. (this is known as limit) Our horizontal asymptote will be at $y=0$. This also helps to determine the domain of this function, since $y\ne 0$. In interval representation.

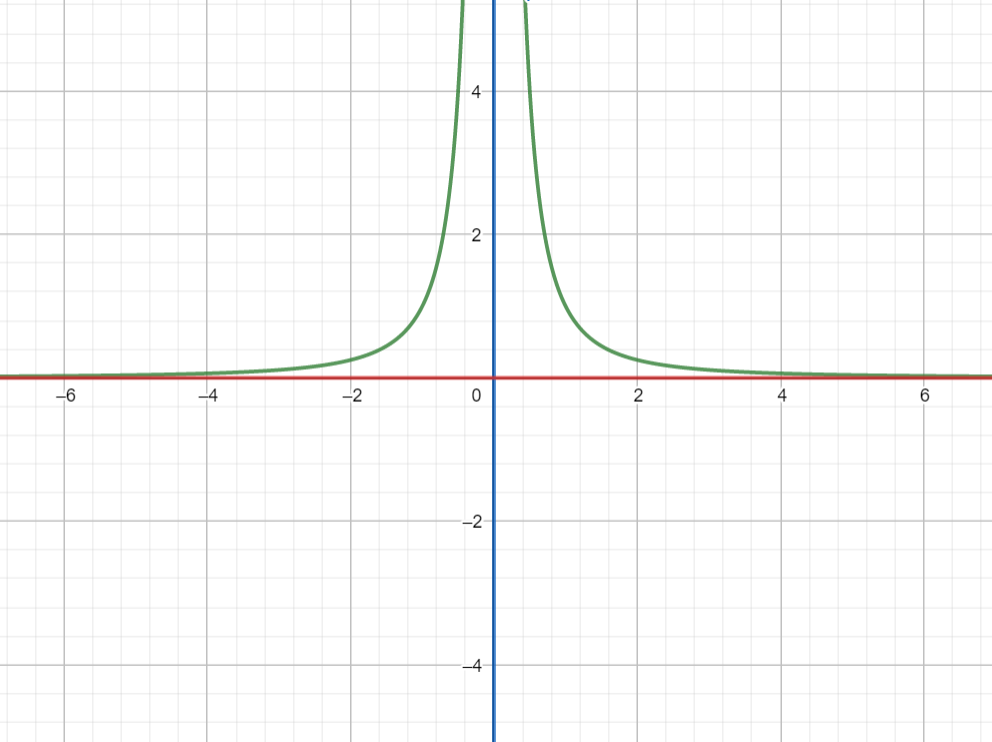
The graph depicts the function and the asymptotes.
Green colour indicates the function $y=\dfrac{1}{{{x}^{2}}}$
Blue colour indicates the vertical asymptote $x=0$
Red colour indicates the horizontal asymptote $y=0$ .

Note: An asymptote is a line that a curve approaches, as it leads to infinity. While drawing the graph always draw the axes first and then mark points and then plot the graph. Note that we can have two times asymptotes. If a line is parallel to x axis, it shows that we have a horizontal asymptote and if a line is parallel to y axis then we have vertical asymptotes.