Question

What are some examples of non-differentiable functions?

Answer 1

Hint : A function $f(x)$ is said to be differentiable, if the derivative of the function exists at every point in its given domain. Geometrically the derivative of a function $f(x)$ at a point $x = {x_0}$ is defined as the slope of the graph of $f(x)$ at $x = {x_0}$ . Then the function is said to be non-differentiable if the derivative does not exist at any one point of its domain.

Complete step-by-step answer :
Some examples of non-differentiable functions are:
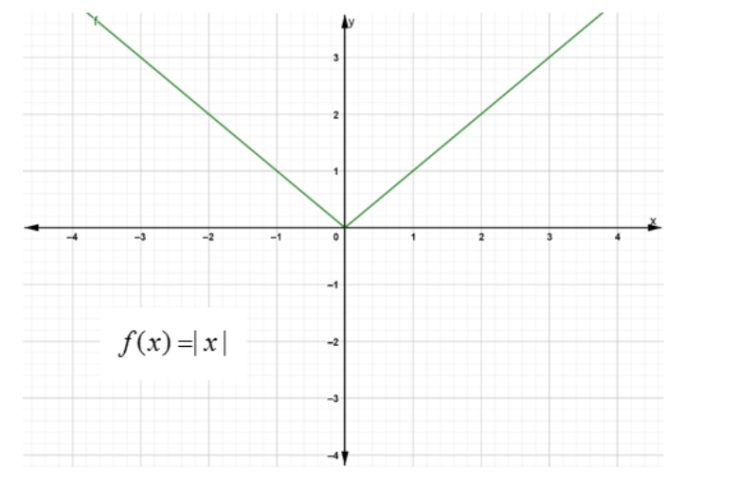
A function is non-differentiable when there is a cusp or a corner point in its graph. For example consider the function $f(x) = |x|$ , it has a cusp at $x = 0$ hence it is not differentiable at $x = 0$ .

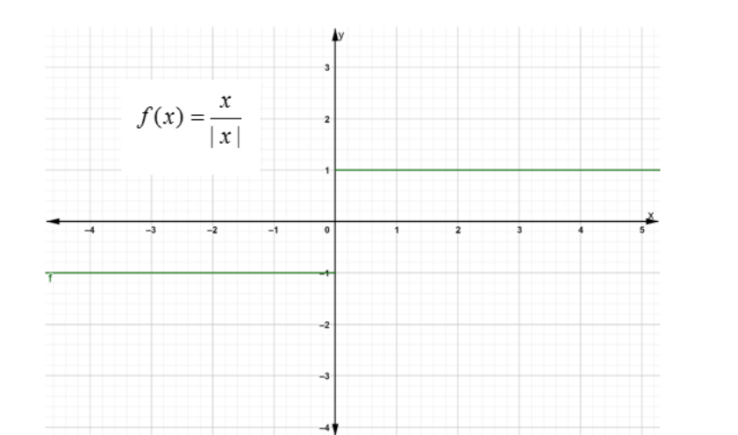
If the function is not continuous then it is not differentiable, i.e. when there is a gap or a jump in the graph of the function then it is not continuous hence not differentiable. For example consider the step function $f(x) = \dfrac{x}{{|x|}}$ , here there is a jump discontinuity $x = 0$ .

                           ![](https://www.vedantu.com/question-sets/619a02d2-e453-485b-9736-4d5bce5bb9f47334629605430970476.png)  

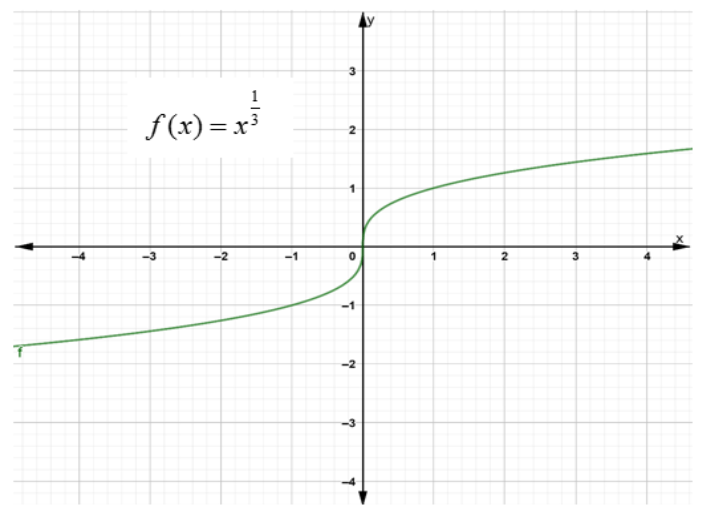
If the function can be defined but its derivative is infinite at a point then it becomes non-differentiable. This happens when there is a vertical tangent line at that point. For example, consider $f(x) = {x^{\dfrac{1}{3}}}$ , it has a vertical tangent line at $x = 0$ , therefore at $x = 0$ its derivative is infinite.

![](https://www.vedantu.com/question-sets/b8e7dc0a-3189-4e75-8bfc-abe145fc3b0f8040085632652324824.png)  

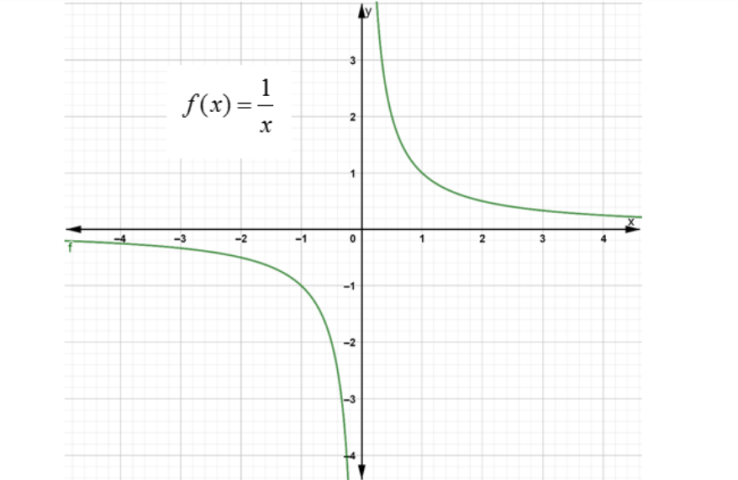
When the function is unbounded and goes to infinity at some point of its domain it becomes non-differentiable. For example consider $f(x) = \dfrac{1}{x}$ which goes to infinity at $x = 0$ , hence non- differentiable

Note : If a function is differentiable then it is always continuous but the converse need not be true, i.e. there are functions which are continuous but not differentiable for example $f(x) = |x|$ is continuous at $x = 0$ but not differentiable at $x = 0$ . By studying the graph of the given function we can easily conclude about the continuity and differentiability of the function.