Question

What are imaginary numbers?

Answer 1

Hint: To solve the given question, we will look at the definition of complex numbers. Then we will find out how it is denoted and what is the general form of complex numbers. Then we will look at the other forms of complex numbers also.

Complete step-by-step answer:
A complex number is a number that can be expressed in the form of a + ib where a and b both are real numbers and ‘i’ is called iota. The ‘a’ is called the real part of the complex number and ‘b’ is the imaginary part of the complex number. Any complex number is generally denoted by the alphabet ‘z’. The general representation of the complex number z = a + ib in a complex plane is shown below,

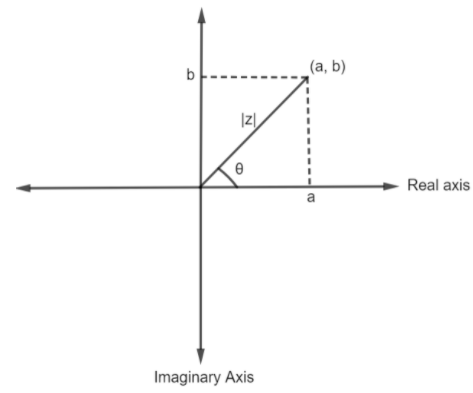
Here, $\theta$ is the angle formed by the complex number from the positive x-axis in the anti-clockwise direction. |z| is the modulus of the absolute value of z and |z| is given by the formula,
$\left| z \right|=\sqrt{{{a}^{2}}+{{b}^{2}}}$
The other forms of the complex number z are shown. The polar form of z is,
$z=r\left( \cos \theta +i\sin \theta \right)$
where r = |z|.
The Euler form of the complex number z is.
$z=r{{e}^{i\theta }}$
All these forms are interconvertible to each other. Hence, A complex number is said to be an imaginary number where we can write a complex number as $a+ib$ and in euler form.

Note: As we know that, z = a + ib and a, b are real numbers. But when a = 0, the number z becomes a purely complex number, and b = 0, the number z becomes a purely real number. So, we can say that b cannot be zero. Also, when we put both a and b as zero, we will get z = 0 which is both purely complex and purely real.